Выравнивание данных
В силу конструктивных ограничений пакетный цикл обмена с памятью не может начинаться с произвольного адреса. В зависимости от типа процессора он автоматически выравнивается по границе 32-, 64- и 128байт на K6/P-II/P-III, Athlon и P-4 соответственно. (см. "Отображение физических DRAM-адресов на логические").
Задумаемся, что произойдет, если на P-III мы запросим двойное слово, лежащее по адресу, равному, ну скажем, 30? Правильно! Для его чтения потребуется выполнить два пакетных цикла! В первом цикле будут загружены ячейки из интервала [(30 % 32); (30 % 32) + 32), т.е. [0; 32), в который входит лишь половина запрошенного нами двойного слова. Для чтения другой его половины потребуется совершить еще один цикл, – [32; 64). В результате, – время доступа к ячейке возрастет как минимум вдвое.
Но не стоит упрекать создателей Pentium'а в кретинизме, – многие процессоры, в отличии от него, вообще запрещают доступ по не выровненным адресам, генерируя при этом исключение! Однако и на Pentium'ах таких ситуации все же рекомендуются избегать. И вот тут самое время рассказать о широко распространенном заблуждении, связанном с выравниванием данных.
Подавляющее большинство руководств по оптимизации (равно как и техническая документация от производителей процессоров) настоятельно рекомендуют всегда выравнивать данные независимо то того, по каким адресам они лежат. На самом же деле, если запрошенные данные целиком умещаются в один пакетный цикл, то величина выравнивания не играет никакой роли! Чтение двойного слова, начинающегося с адреса 0x40001, осуществляется безо всяких задержек (no penalty!), поскольку оно гарантированно не пересекает пакетный цикл. Действительно, 0x20 – (0x40001 % 0x20) == 0x1F, а 0x1F > sizeof(DWORD) /* в смысле расстояние до правой границы пакетного цикла превышает размер читаемых данных */! Следовательно, чтение двойного слова с адреса 0х40001 вполне законно, хотя он (адрес) отнюдь и не кратен 4.
Подробный разговор о проблемах выравнивания мы отложим на потом (см. "Кэш. Выравнивание данных"), поскольку он больше относится к кэшу, чем к подсистеме оперативной памяти, здесь же мы рассмотрим лишь влияние начального адреса на скорость обработки больших блоков памяти (см. [Memory/align.c]).
Достаточно очевидно, что при линейной обработке памяти кратность выравнивания начального адреса играет второстепенную роль. Действительно, если очередная порция запрошенных данных "вылетит" за пределы пакетного цикла и процессор будет вынужден инициировать еще один цикл обмена, – мы не слишком огорчимся этим обстоятельством, поскольку эти данные нам все равно предстоит загружать. Так какая разница, – случится это раньше или позже?
На самом деле, некоторая разница все же есть. При чтении данных, пересекающих пакетный цикл, процессор вынужден тратить по крайней мере один такт, на склеивание двух половинок данных, что несколько ухудшит производительность. Впрочем, ненамного: на ~10% на P-III, и на ~20 на AMD Athlon (см. рис. graph 34). В подавляющем большинстве случаев этой величиной можно безболезненно пренебречь. Тем нее менее, если вы хотите достичь максимальной производительности, соответствующим образов выравнивайте адреса (см. таблицу 2 ниже).
|
Размер данных |
Граница |
|
1 байтов (8 битов) |
Произвольная |
|
2 байтов (16 битов) |
Кратная 2 байтам |
|
4 байтов (32 бита) |
Кратная 4 байтам |
|
8 байтов (64 битов) |
Кратная 8 байтам |
|
10 байтов (80 битов) |
Кратная 16 байтам |
|
16 байтов (128 битов) |
Кратная 16 байтам |
Совершенно иная ситуация с записью данных. Механизм отложенной записи, реализованный в процессорах Pentium и AMD Athlon, предотвращает падание производительности вызванное несовпадением размером записываемых данных с границами пакетных циклов. На P?III запись не выровненных данных выполняется всего лишь на 3% медленнее, а на AMD Athlon даже на 35% быстрее! Нет, это не ошибка! В силу конструктивных особенностей процессора Athlon и северного моста чипсета VIA KT133, запись не выровненных данных действительно осуществляется значительно быстрее.
Однако данный эффект наблюдается исключительно при записи данных в оперативную память. Не выровненная запись в кэш-память несет значительные издержки, многократно снижая производительность (см. "Кэш. Выравнивание данных"), поэтому пренебрегать выравниванием допускается только
при обработке огромных блоков памяти (от 1 Mб и выше), многократно превосходящих в объеме емкость кэшей всех уровней.
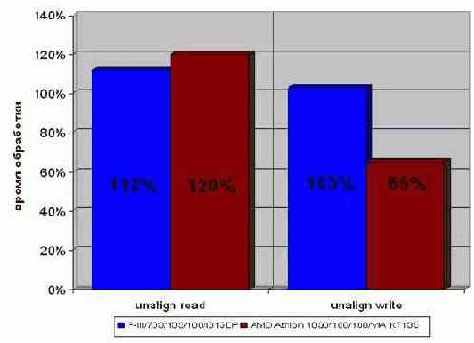
Рисунок 35 graph 026 Эффективность выравнивания начального адреса при обработке больших массивов данных. Не выровненный начальный адрес читаемого потока памяти несет ~15% издержки производительности. Записывание данных, напротив, не требует выравнивания, а на AMD Athlon не выровненные данные обрабатываются даже быстрее
В заключении рассмотрим какое влияние на производительность оказывает выбор адресов источника и приемника при копировании больших блоков памяти (см. [memory/align.memcpy]. Как нетрудно догадаться, выравнивание адреса-приемника не имеет решающего значения, а вот неудачный выбор адреса-источника заметно снижает быстродействие программы. И это действительно так! (см. рис. graph 27).
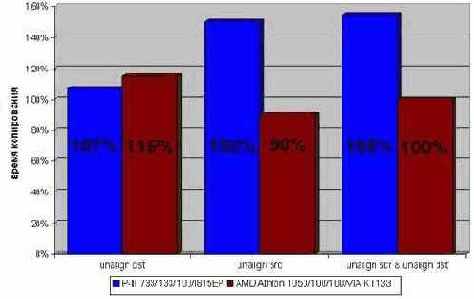
Рисунок 36 graph 27 Влияние на производительность выравнивания адресов источника и приемника при копировании памяти. Главное – выровнять источник. Выравниванием же начального адреса приемника можно пренебречь
Техника ручного выравнивания данных
Штанных средств выравнивания данных (подробнее см. "Кэш. Выравнивание") очень часто оказывается недостаточно. Во-первых, они действуют только на элементы структур, а локальные и глобальные переменные компилятор всегда выравнивает по собственному усмотрению, и, во-вторых, максимально допустимая степень выравнивания обычно (читай у Microsoft Visual C++ и Borland C++) ограничена кратностью в 16 байт. Т.е. выровнять массив по границе кэш-линий (32 байта для P–III и 64 байта для Athlon) не удастся! /* ну почему же не удастся? еще как удастся – см. "Кеш.
Выравнивание" */ Некоторые руководства (в том числе и довольно авторитетные) рекомендуют в этой ситуации прибегать к ассемблеру. Что ж, ассемблер – действительно, великая вещь, но как быть тем, кто им не владеет? (А не владеют ассемблером большинство прикладных программистов)
Однако для решения этой задачи вполне достаточно штатных средств языка Си. Поскольку, 32-битные near-указатели представляют собой по сути 32-битные целые, – весь математический аппарат к услугам программиста. Фактически решение задачи сводится к следующему: есть число X, из него надо получить число Y, максимально близкое к X и кратное N. Первое, что приходит на ум: Y = (X / N)*N. Если N не любое число, а кратное степени двойки, то от медленной операции деления можно отказаться, вручную сбрасывая соответствующий двоичный разряд с помощью логического AND. Так же, будет необходимо увеличить "усеченный" указатель на величину, равную степени выравнивания, т.к. при выравнивании происходит уменьшение указателя, в результате чего он залезает в чужую область. Естественно, количество выделяемой памяти придется увеличить на величину округления. Таким образом, законченное решение будет выглядеть приблизительно так:
char p;
p = (char*) malloc(need_size + (align_powr – 1));
p = (char *) (((int)p + align_power – 1) & ~(align_power - 1));
где align_power – требуемая степень выравнивания, а "char*" – тип указателя (естественно, не обязательно именно char* – это может быть и int*)
Тот же трюк может использоваться и при выравнивании массивов, расположенных в стеке или сегменте данных. Например:
#define array_size 1024
#define align_power 64
int a[array_size + align_power –1];
int *p;
p = (int *) (((int)&a + align_power – 1) & ~(align_power-1));
Указатель 'p' будет указывать на начало массива, выровненного по 64-байтной границе (такое выравнивание обеспечивает наиболее эффективную обработку данных – см. "Кэш.
Использование упреждающего чтения").
Кстати, при желании массив можно использовать и для хранения разнотипных данных, выравнивая их так, как это заблагорассудится. Например:
char array[9];
#define a array[0]
#define b (int *array[sizeof(char)])[0]
#define c (int *array[sizeof(char)+sizeof(int)])[0]
#define d (int *array[sizeof(int)*3])[0]
Этот, пускай и не очень изящный, трюк позволяет хранить переменные вплотную друг к другу, без зазоров и контролировать их порядок размещения в памяти, что позволяет, например, рассовать совместно используемые переменные по разным банкам. Дело в том, что локальные переменные размещаются в стеке не в порядке их объявления в программе, а как это заблагорассудиться компилятору.
Выравнивание потоков данных. Если с выравниванием блоков памяти, возвращенных malloc, все более или менее понятно (действительно, это очень простая задача), то выравнивание адресов, получаемых функцией извне, несколько сложнее. Рассмотрим следующий пример: пусть нам необходимо посчитать сумму всех элементов некоторого массива. Проще всего это сделать приблизительно так:
int sum(int *array, int n)
{
int a, x = 0;
for(a = 0; a < n; a++)
x+=array[a];
return x;
}
Листинг 24 Не оптимизированный пример реализации функции. *array может быть не выровнен!
Недостаток предложенной реализации в том, что она никак не заботится о выравнивании данных, молчаливо перекладывая эту заботу на плечи вызывающего ее кода. А это весьма рискованное допущение! Даже если мы явно оговорим целесообразность выравнивания в спецификации функции, использующий ее программист может просто пренебречь (забыть, упустить) этой рекомендацией. К тому же не всегда возможно выровнять передаваемый функции адрес (скажем, программист сам получил его не выровненным извне).
Поэтому, заботиться о выравнивании адресов вызываемая функции должна самостоятельно. В состоянии ли она это сделать? На первый взгляд нет.
Легко доказать, что если (x & 3) != 0, то и ((x + sizeof(int)*k) & 3) != 0. Действительно, это так, но… в том-то и все и дело, что штрафные такты за доступ по не выровненным данным даются лишь в том, и только в том случае когда они пересекают границы пакетных циклов обмена. А вот на этом можно и сыграть!
Читаем память двойными словами до тех пор, пока текущий адрес (((p % BRST_LEN) + sizeof(DWORD)) < BRST_LEN), – т.е. пока мы не дойдем до двойного слова, пересекающего границы пакетных циклов обмена. "Опасный" участок трассы проходим маленькими – побайтовыми – шажками, что гарантированно страхует нас от почетной "награды" в виде пенальти. Остается лишь собрать эти четыре байта в одно слово, что элементарно осуществляется битовыми операции сдвига. Затем описанный цикл чтения вновь повторяется (см. рис. 45). И так происходит до тех пор, пока не будет достигнут конец обрабатываемого блока памяти.
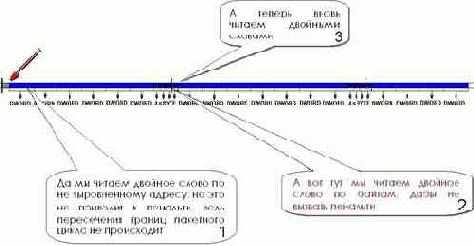
Рисунок 37 45 Техника эффективной обработки не выровненного двухсловного потока данных
Одна из возможных реализаций предложенного алгоритма показана ниже. Обратите внимание: общих решений поставленная задача не имеет. Максимальное количество двойных слов в типичном пакете всего восемь, а при работе с не выровненными адресами и того меньше! Цикл из нескольких интеракций – крайне медленная штука и во избежание падения производительности он должен быть развернут целиком. В этом-то и заключается основная проблема: поскольку количество итераций зависит от величины смещения указателя в пакетном цикле обмена, нам необходимо создать BRST_LEN – BRST_LEN/sizeof(DWORD) различных циклов, каждый из которых будет обрабатывать "свое" смещение указателя. Для экономии места в книге ### приведен лишь один вариант, поскольку остальные реализуются практически аналогично.
// -[Посечет суммы массива]----------------------------------------------------
//
// ARG:
// array - указатель на массив
// n - кол-во элементов для сортировки
//
// README:
// Функция справляется с не выровненными массивами, и сама выравнивает их
// (правда, было бы лучше, если бы она это не делала)
//----------------------------------------------------------------------------
int sum_align(int *array, int n)
{
int a, x = 0;
char supra_bytes[4];
// внимание: это решения для _частного_ случая
// когда array & 15== 1, т.е. попросту говоря,
// указатель смещен на 1 байт вправо относительно
// выровненного по границе 32 байт адреса
// общее решение данной задачи без использования
// циклов (циклы - снижают производительность)
// невозможно!
// единственный вариант - вручную создать свой
// "обработчик" для каждой ситуации
// всего их будет 32 - 32/4 = 24, что слишком
// громоздко для книжного варианта
if (((int)array & 15)!=1)
ERROR("-ERR: Недопустимое выравнивание\n");
for(a = 0; a < n; a += 8)
{
// копируем все двойные слова, которые
// не пересекают границы пакетных циклов
// обмена
x+=array[a + 0];
x+=array[a + 1];
x+=array[a + 2];
x+=array[a + 3];
x+=array[a + 4];
x+=array[a + 5];
x+=array[a + 6];
// двойное слово, пересекающие пакетный цикл
// копируем во временный буфер по б а й т а м
supra_bytes[0]=*((char *) array + (a+7)*sizeof(int) + 0);
supra_bytes[1]=*((char *) array + (a+7)*sizeof(int) + 1);
supra_bytes[2]=*((char *) array + (a+7)*sizeof(int) + 2);
supra_bytes[3]=*((char *) array + (a+7)*sizeof(int) + 3);
// извлекаем supra-байты и обрабатываем их как двойное слово
x+=*(int *)supra_bytes;
}
return x;
}
Листинг 25 [Memory/align.dwstream.c] Пример реализации эффективной обработки не выровненного двухсловного потока данных
И вот тут нас ждет неожиданный и весьма неприятный сюрприз. "Оптимизированная" программа выполняется намного медленнее
первоначального варианта! На P?III 733/133/100/I815EP падение производительности составляет ~15%, а на AMD Athlon 1050/100/100/VIA KT133… аж ~130%!!! Ничего себе "оптимизация"! В чем же причина? Дело в том, что предотвращение пересечения пакетных циклов обмена достается нам дорогой ценой, а именно – увеличением количества обращений к памяти. Это-то и снижает производительность!
Тем не менее, автор отнюдь не собирается выбрасывать предложенный алгоритм на помойку. Тут еще есть над чем подумать! "А почему бы нам ни подумать вместе?" (с) Котенок Гав.
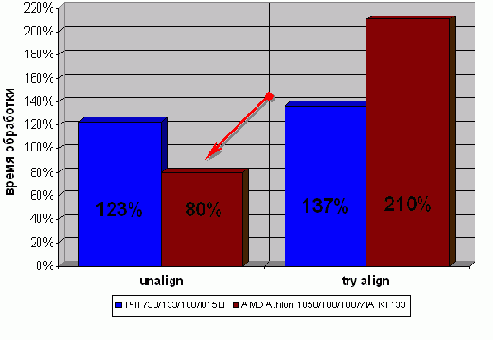
Рисунок 38 graph 34 Описанная методика "эффективной" обработки не выровненного двухсловного потока данных, на самом деле снижает производительность. Самое интересное, что не выровненный поток на AMD Athlon обрабатывается даже быстрее, чем выровненный!
Выравнивание байтовых потоков данных.
Эффективная обработка байтовых потоков данных двойными словами (см. "Обработка памяти байтами, двойными и четвертными словами") возможна лишь в том случае, если адрес начала блока выровнен по границе четырех байт. А так, к сожалению, бывает не всегда. Ведь байтовые потоки не требуют выравнивания по определению и компилятор (или программист) может располагать их по любому месту в памяти – где ему больше заблагорассудиться. К счастью, самостоятельно выровнять такой поток вызываемой функции не составит большого труда!
Поскольку байтовый поток однороден мы можем начать читать его с любого места. Вычисляем адрес ближайшей границы пакетного цикла (в общем случае он равен p + (BRST_LEN ? ((int) p % BRST_LEN))) и гоним двойными словами в полную силу, не забывая, конечно, о том, что размер блока не всегда бывает кратен sizeof(DWORD).
Постойте! А как же первые (BRST_LEN ? ((int) p % BRST_LEN)) байтов?! Ведь они остались необработанными! Что ж, добавить дополнительный цикл обработки – не проблема! (см. рис. 46)
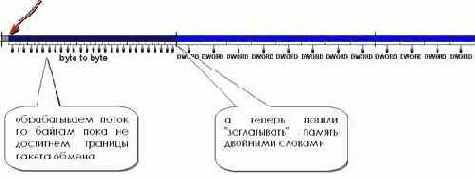
Рисунок 39 46 Техника выравнивания байтовых потоков данных. В отличии от выравнивая двухсловных потоков, она действительно эффективна
Возвращаясь к листингу 23, реализующему простейший шифровальный алгоритм, давайте научим его выравнивать обрабатываемый блок данных. Один из возможных способов приведен ниже:
// -[Simple byte-crypt]-------------------------------------------------------
//
// ARG:
// src - указатель на шифруемый блок
// mask - маска шифрования (байт)
//
// DEPENCE:
// unalign_crypt
//
// README:
// функция самостоятельно выравнивает шифруемые данные
//----------------------------------------------------------------------------
void align_crypt(char *src, int n, int mask)
{
int a;
char *x;
int n_ualign;
// вычисляем величину на которую следует "догнать" блок
// чтобы он стал выровненным блоком
n_ualign= 32 - ((int) src & 15);
// шифруем пока не достигнем границы пакетного цикла обмена
unalign_crypt(src, n_ualign, mask);
// смело шифруем все остальное
// т.к. src+n_ualign - гарантированно выровненный указатель!
unalign_crypt(src+n_ualign, n-n_ualign, mask);
/* не забываем уменьшить ^^^^^^^^^^^^ ко-во шифруемых байтов */
}
Листинг 26 [Memory/align.bstream.c] Пример реализации функции, самостоятельно выравнивающий байтовый поток данных
Прогон программы показывает, что оптимизированный вариант с одинаковой эффективностью обрабатывает как выровненные так и не выровненные блоки данных, в то время как не оптимизированный теряет на не выровненных блоках от ~17% до 69% производительности (на P-III 733/133/100/I815EP и AMD Athlon 1050/100/100/VIA KT 133 соответственно).
Кстати, функция align_crypt (как вы, наверное, уже обратили внимание) представляет собой не более чем "обертку" для unalign_crypt, т.е. она легко может быть адоптированная под ваши собственные нужды. Для этого достаточно лишь заменить вызов "unalign_crypt" на вызов вашей функции.
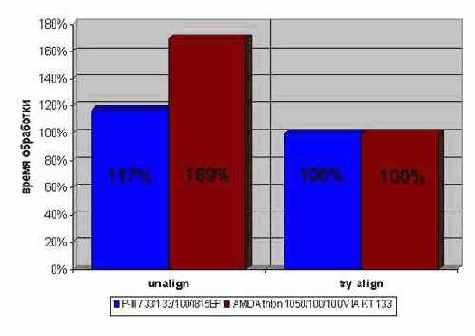
Рисунок 40 graph 35 Демонстрация эффективности выравнивания байтовых потоков данных. Легко видеть, что предложенная техника выравнивания на 100% эффективна