Влияние размера обрабатываемых данных на производительность
Никто не спорит, – чем меньше массив данных, тем быстрее он обрабатывается – это общеизвестно. Для достижения наивысшей производительности следует проектировать алгоритм программы так, чтобы все интенсивно обрабатываемые блоки данных целиком умещались в сверхоперативной памяти первого или, на худой конец, второго уровня. В противном случае обмен с оперативной памятью в мгновение ока сожрет все мегагерцы процессора.
Но, вот вопрос, – какой именно зависимостью связан размер с производительностью? В частности: на сколько упадает быстродействие программы, если обрабатываемый блок данных вылезет за переделы кэш-памяти первого (второго) уровня, ну скажем, на один килобайт? Еще вопрос: весь ли объем кэша доступен для непосредственного использования или некоторую его часть необходимо резервировать для хранения стековых переменных, аргументов и адреса возврата из функции? Популярные руководства по оптимизации хранят гробовое молчание на этот счет, в основном ограничиваясь сухим правилом "кто не вместился в кэш – том сам себе и виноват".
Даже такой авторитет как Agner Fog в свей монографии "How to optimize for the Pentium family of microprocessors" приводит всего лишь ориентировочное количество тактов, требующихся для загрузки ячейки из различных иерархий памяти! Может быть, эта информация и полезна сама по себе, но она не дает общего представления о картине. Ведь "время доступа" как уже было показано в первой части настоящей книги (см. Части I "Оперативная память. Взаимодействие памяти и процессора. Вычисление полного времени доступа") – слишком абстрактное понятие, тесно переплетающееся с конвейером и параллелизмом. К тому же, Fog устарел не на один ледниковый период и сегодня представляет разве что исторический интерес (во всяком случае – часть, касающаяся времени доступа к памяти). Что ж! Ничего не остается как затовариться пивом (или "Напитками из Черноголовки" – это кому как во вкусу) и плотно засесть за компьютер в надежде разобраться во всем самостоятельно.
Давайте напишем следующую тестовую программку, обрабатывающую в цикле блоки все большего и большего размера, а затем выведем полученные результаты в виде графика на экран. При этом мы исследуем четыре основных комбинации обработки данных: последовательное чтение, последовательная запись, чтение ячейки с последующей модификацией и запись ячейки с последующим чтением. Конечно, не мешало бы исследовать еще и параллельную обработку (см. "Часть I. Оптимизация работы с памятью. Параллельная обработка данных"), но – боюсь – что в этом случае размер книги превысил бы все мыслимые барьеры…
#define BLOCK_SIZE (715*K) // размер обрабатываемого блока памяти
#define STEP_FACTOR (1*K) // шаг приращения перебираемого размера
#define X 1 // :'b' - для вычитания линейной составляющей
// :'1' - показывать график как есть
// выделяем память
p = malloc(BLOCK_SIZE);
// шапка
printf("---\t");
for (b = 1*K; b < BLOCK_SIZE; b += STEP_FACTOR)
printf("%d\t",b/K); printf("\n");
/*------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНОЕ ЧТЕНИЕ
*
---------------------------------------------------------------------- */
printf("R\t"); for (b = 1*K; b < BLOCK_SIZE; b += STEP_FACTOR)
{
PRINT_PROGRESS(25*b/BLOCK_SIZE); VVV;
A_BEGIN(0)
for (c = 0; c <= b; c += sizeof(int))
tmp += *(int*)((int)p + c);
A_END(0)
printf("%d\t", 100*Ax_GET(0)/X);
}
printf("\n");
/*------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНАЯ ЗАПИСЬ
*
---------------------------------------------------------------------- */
printf("W\t"); for (b = 1*K; b < BLOCK_SIZE; b += STEP_FACTOR)
{
PRINT_PROGRESS(25+25*b/BLOCK_SIZE); VVV;
A_BEGIN(1)
for (c = 0; c <= b; c += sizeof(int))
*(int*)((int)p + c) = tmp;
A_END(1)
printf("%d\t", 100*Ax_GET(1)/X);
}
printf("\n");
/*------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНОЕ ЧТЕНИЕ потом ЗАПИСЬ
*
---------------------------------------------------------------------- */
printf("RW\t"); for (b = 1*K; b < BLOCK_SIZE; b += STEP_FACTOR)
{
PRINT_PROGRESS(50+25*b/BLOCK_SIZE); VVV;
A_BEGIN(2)
for (c = 0; c <= b; c += sizeof(int))
{
tmp += *(int*)((int)p + c);
*(int*)((int)p + c) = tmp;
}
A_END(2)
printf("%d\t", 100*Ax_GET(2)/X);
}
printf("\n");
/*------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНОЕ ЧТЕНИЕ потом ЗАПИСЬ
*
---------------------------------------------------------------------- */
printf("WR\t"); for (b = 1*K; b < BLOCK_SIZE; b += STEP_FACTOR)
{
PRINT_PROGRESS(75+25*b/BLOCK_SIZE); VVV;
A_BEGIN(3)
for (c = 0; c <= b; c += sizeof(int))
{
*(int*)((int)p + c) = tmp;
tmp += *(int*)((int)p + c);
}
A_END(3)
printf("%d\t", 100*Ax_GET(3)/X);
}
printf("\n");
Листинг 1 [Cache/cache.size.c] Пример, демонстрирующий зависимость времени обработки от размера и рода обработки блока данных
Вид полученного графика может варьироваться в зависимости от архитектуры используемого процессора, но в целом должен выглядеть приблизительно так, как показано на рис. graph 0x0. Ага! Вот он потерянный хвост Иа! Если скоростная кривая чтения ячеек (синяя линия) напоминает обветшалый и разрушенный эрозией старый пологий холм, то остальные кривые являют собой молодую горную формацию, непрерывно
меняющую крутизну своих склонов.
Если присмотреться повнимательнее (впрочем, вряд ли вы что разглядите на полиграфии такого качества), то можно заметить, что первый подъем расположен в районе ~32 километра, ой, я хотел сказать килобайта. Это и есть размер сверхоперативной памяти кэша данных первого уровня микропроцессора AMD K6 (кстати, неплохого между прочим процессора).
Миновав кэш, график чтения начинает линейное восхождение вверх с коэффициентом пропорциональности близким к единице, т.е. на участке (L1.CACHE.SIE; L2.CACHE.SIZE] – время обработки блока в зависимости от его размера изменяется так: , где T – время обработки. При выходе за пределы кэша первого уровня быстродействие программы резко и значительно сокращается, – действительно, по горам лазать – это вам не по равнине налегке ходить (кэш первого уровня – это равнина).
Наклон графика чтения задирается к верху еще круче и визуально (то бишь субъективно) его коэффициент пропорциональности близко к полутора, а то и двум. Между тем, это – не более чем досадный обман зрения и формула зависимости времени обработки от размеров записываемого блока идентична формуле чтения. Не верите? Так давайте проверим! Смотрите: обработка ~89 Кб блока данных заняла 200.000 тактов процессора, а ( …приложив линейку к монитору…) блок в ~177 Кб обрабатывался бы 400.000 тактов. А теперь – 89 : 177 ==200.000 : 400.000 == 0.5, что и требовалось доказать!
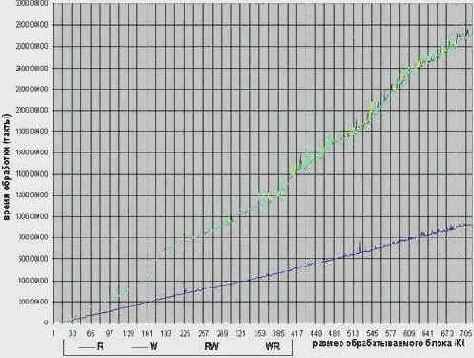
Рисунок 17 graph 0 Зависимость времени обработки от размера блока (AMD K6) без вычета линейной составляющей
Увы, мы должны признать, что наглядность полученного нами графика оставит желать лучшего. Причина в том, что он состоит из двух составляющих. Линейный
рост времени обработки возникает вследствие увеличения количества операций обращения к памяти. На него наложена нелинейная
составляющая, обусловленная непостоянством скорости доступа к различным видам памяти.
Поскольку, в данном случае нас интересует именно скоростной показатель доступа к памяти, а не общее время обработки блока данных, от линейной составляющей мы должны избавится.Если не требуется большой точности вычислений, достаточно разделить результаты каждого замера на число итераций цикла. (Примечание: на самом деле, это очень большое упрощение. Время обработки блока данных равно N*(Tcycle +T
В результате, форма полученного графика должна выглядеть приблизительно так:
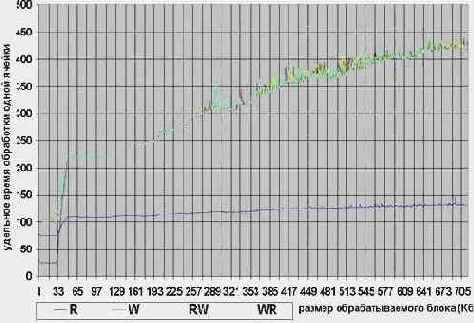
Рисунок 18 graph 1 Зависимость скорости обработки от размера блока на AMD K6