Учет ограниченной ассоциативности кэша
До тех пор, пока в процессорах не появятся полностью ассоциативные кэши, оптимальная организация данных останется прерогативой программистов. В главе "Кэш – принципы функционирования: Организация кэша" было показано, что каждая ячейка кэшируемой памяти может претендовать не на любую, а всего лишь на несколько кэш-строк, число которых и определяется ассоциативностью кэша. Поскольку, ассоциативность кэш-памяти первого уровня обычно очень невелика (так, на P-II/P-III она равна четырем, а на AMDAthlon и вовсе двум), становится очевидным, что неудачная организация данных способна сократить размер кэш-памяти на один-два порядка, а то и более того!
Если установочные биты кэшируемых ячеек равны, они отображаются на одну и ту же кэш-строку, поэтому таких ситуаций следует избегать. Как вычисляются установочные адреса? Для этого можно воспользоваться следующей формулой. set.address = my.address & ((mask.bank – 1) & ~(mask.line-1)), где mask.line (маска кэш линей) определяется так: 2mask.line = CACHE.LINE.SIZE, а mask.bank (маска банка) определяется так: 2mask.bank == BANK.SIZE. В частности, 4х ассоциативный 16 Кб кэш процессоров P-II/P-III задействует под установочные адреса биты с 11 по 4 линейного адреса памяти.
Таким образом, обработка ячеек памяти с шагом равным или кратным размеру кэш банка крайне непроизводительна и этого любой ценой следует избегать. Касательно размера кэш-банков – позвольте поделиться наблюдением: на всех известных мне процессорах он равен или кратен 4 Кб. Эта цифра, конечно, не догма (см. "Определение ассоциативности"), но как рабочий вариант вполне сойдет.
А теперь скажите, как вы думаете, можно ли назвать следующий код оптимальным кодом?
for(a = 0; a < googol; a++)
{
// …
a1 += bar[4096*1];
a2 += bar[4096*2];
a3 += bar[4096*3];
a4 += bar[4096*4];
a5 += bar[4096*5];
// …
}
Листинг 7 Пример, демонстрирующий конфликт кэш-линеек за счет ограниченной степени ассоциативности
Увы, оптимальность здесь и не ночевала. Смотрите, что происходит: при исполнении программы под P-II/P-III: в первом проходе цикла for ячейки bar[4096]
еще не содержится в сверхоперативной памяти первого уровня и возникает задержка в два-четыре такта, на время загрузки данных из кэша второго уровня (а в худшем случае – из оперативной памяти). Поскольку установочный адрес ячейки равен нулю (условимся считать, что массив bar выровнено по 4 Кб границе, хотя это и не критично), кэш контроллер помещает считанные 32 байта в нулевую кэш-строку первого (точнее, условного первого) кэш-банка. Идем далее: установочный адрес ячейки bar[4096*2]
тоже равен нулю и очередная порция считанных данных также претендуют на нулевую кэш-строку! Поскольку, нулевая строка первого кэш-банк уже занята, кэш-контроллер задействует второй банк…
Но ведь количество кэш-банков не безгранично! Напротив, – оно очень мало, и на момент чтения пятой по счету ячейки – bar[4096*5]
нулевые кэш-строки всех четырех кэш- банков уже заняты, а данная ячейка претендует именно на нулевую кэш-строку! Кэш-контроллер (а что ему еще остается делать?) безжалостно "прибивает" наиболее "дряхлую" нулевую строку первого кэш-банка (к ней дольше всего не было обращения) и записывает в нее "свежие" данные. Как следствие – в следующем проходе цикла for ячейки bar[4096]
вновь не оказывается в сверхоперативной памяти первого уровня, и вновь возникнет задержка на время ее загрузки! Кэш контроллер, обнаружив, что свободных банков совсем нет (помните как в том анекдоте про бензин "Как нет? Совсем нет, да!"), прибивает нулевую строку теперь уже второго банка – ту, что хранила ячейку bar[4096*2]… Чувствуете, что происходит? Правильно, кэш работает на 100% вхолостую, не обеспечивая ни одного кэш-попадания – одни лишь промахи. А ведь обрабатываемых ячеек памяти всего лишь пять…
Во избежании падения производительности, обрабатываемые данные необходимо реорганизовать так, чтобы читаемые ячейки попадали в различные кэш-линии, а, если это невозможно, то обрабатывать их не в одном, а в нескольких последовательных циклах, например, так:
for(a = 0; a < googol; a++)
{
// …
a1=bar[4096];
a2=bar[4096*2];
a3=bar[4096*3];
// …
}
for(a = 0; a < googol; a++)
{
// …
a4=bar[4096*4];
a5=bar[4096*5];
// …
}
Листинг 8 Оптимизированный вариант программы, учитывающий особенности архитектуры наборно-ассоциативной кэш памяти
А теперь разберем как будет исполняться следующий код на процессоре AMD Athlon. На первый взгляд, все произойдет по сценарию, описанному выше, с той лишь разницей, что двух ассоциативный кэш Athlon'а "завалится" уже на третий итерации.
Точнее, мы думаем, что он "завалится", на самом же деле, никакого сколь ни будь заметного падения производительности не наблюдается.
for(a = 0; a < googol; a++)
{
// …
a1 += bar[4096];
a2 += bar[4096*2];
a3 += bar[4096*3];
a4 += bar[4096*4];
a5 += bar[4096*5];
// …
}
Листинг 9 Пример кода, вопреки "здравому смыслу" оптимальное для процессора AMD Athlon
Первое впечатление: Вот это номер! Ай да Athlon! Второе впечатление (немного остынув от щенячьего восторга, мы задаемся известным вопросом): но почему? Как это реализовано? Прочитав руководство по оптимизации от начала до конца, в приложении "А" мы находим междустрочный ответ на вопрос. Оказывается в процессорах AMD Athlon имеется очередь чтения/записи на 12 входов, которая временно сохраняет данные, считанные из кэша первого уровня. Конфликты кэш-линий все-таки возникают, но они маскируются системой буферизации данных. Выходит, что при оптимизации программы исключительно под Athlon нехватки ассоциативности можно не опасаться? Увы, не все так радужно… В данном случае падения производительности не наблюдается лишь только потому, что количество одновременно обрабатываемых ячеек не превышает двенадцати.
Особенно щепетильным следует быть при выборе величины шага чтения при обработке блочных алгоритмов. Если она окажется кратной размеру кэш-банка (или хотя бы производной от него), – многократного падения производительности не избежать.
Рассмотрим следующий пример:
#define N_ITER 466 // кол-во итераций
// теоретически будет востребовано
// LINE_SIZE*N_ITER байт кэш-памяти,
// т.е. в данном случае 466*64 = ~30 Kb
#define CACHE_BANK_SIZE (4*K ) // размер кэш-банка
#define LINE_SIZE 64 // максимально возможный размер кэш-линий
#define BLOCK_SIZE ((CACHE_BANK_SIZE+LINE_SIZE)*N_ITER) // размер бурка
/*----------------------------------------------------------------------------
*
* ВАРИАНТ, ИЛЛЮСТРИРУЮЩИЙ КОНФЛИКТЫ КЭШ-ЛИНИЙ
*
----------------------------------------------------------------------------*/
int over_assoc(int *p)
{
int a;
volatile int x=0;
// внимание: top-level цикл поскипан, поскольку профайлер
// и без того прокрутит этот цикл 10 раз
for(a=0; a < N_ITER; a++)
// читаем память с шагом 4 Kb, в результате
// и на P-II/P-III/P-4 и на AMD Athlon
// быстро наступает насыщение кэша и идет
// его перегруз;
// поскольку, обрабатывается более 12 ячеек
// буферизация чтения на Athlon положения
// уже не спасает
x+=*(int *)((int)p + a*CACHE_BANK_SIZE);
return x;
}
Листинг 10 [Cache/L1.overassoc] Пример, демонстрирующий возникновение конфликтов кэш-линий и их влияние на производительность
При шаге чтения, равным четырем килобайтам, данная программа будет "буксовать" на всех процессорах, поскольку в кэш-память не поместится вообще ни одной ячейки! (Чу! Слышу голоса: "почему ни одной ячейки? Ведь должны же сохранится четыре ячейки на P-II/P-III и две – на Athlon, в соответствии с величиной их ассоциативности". Увы! При очередном проходе цикла последние сохраненные ячейки будут выкинуты из кэша).
Как можно предотвратить кэш-конфликты? Для этого мы должны реструктурировать обрабатываемый массив с таким расчетом, чтобы установочные адреса всех загружаемых ячеек были бы различны. Один из возможных путей решения – увеличить величину шага на размер кэш-линейки. (Конечно, для этого необходимо изменить и сам массив, т.к. при этом будут читаться уже другие
данные).
Оптимизированный пример может выглядеть приблизительно так:
/*----------------------------------------------------------------------------
*
* ВАРИАНТ, ИСПОЛНЯЮЩИЙСЯ БЕЗ КОНФЛИКТОВ
*
----------------------------------------------------------------------------*/
int optimize(int *p)
{
int a=0;
volatile int x=0;
// внимание: top-level цикл поскипан, поскольку профайлер
// и без того прокрутит этот цикл 10 раз
for(a=0; a < N_ITER; a++)
{
// читаем паять с шагом CACHE_BANK_SIZE+LINE_SIZE
// т.е. в данном случае 4096+64=4160 байт;
// поскольку установочные адреса всех ячеек различны
// мы не имеем конфликтов и использует емкость
// кэш-память на все 100%
x+=*(int *)((int)p + a*(CACHE_BANK_SIZE+LINE_SIZE));
}
return x;
}
Листинг 11 [Cache/L1.overassoc.c] Оптимизированный пример, устраняющий конфликты кэш-линий
Прогон программы показывает, что в результате оптимизации ее скорость увеличилась более, чем в шесть раз на процессоре P-III 733 и более чем в пять раз на процессоре AMD Athlon 1050. Согласитесь, очень неплохая прибавка к производительности и это при том, что мы только читали конфликтующие ячейки, но не модифицировали их. Конфликт же записи обойдется вам приблизительно в полтора раза "дороже"!
Поэтому, если ваша программа не смотря на крошечный размер обрабатываемых данных работает на удивление медленно, – в первую очередь проверьте, – не замешен ли здесь конфликт кэш-линеек.
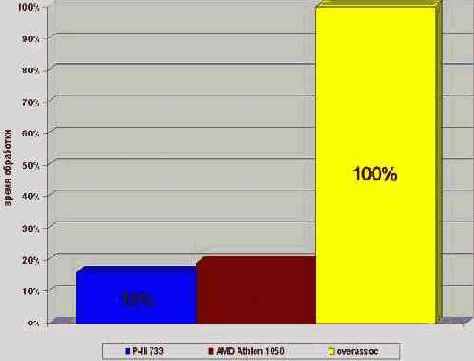
Рисунок 30 graph 0x010 Демонстрация падения производительности при попадании загружаемых данных в одну и ту же кэш-линейку. Конфликт записи обходится приблизительно в полтора раза дороже.