Стратегия распределения данных по DRAM-банкам
Сформулированное в конце предыдущего параграфа правило ориентировано исключительно на потоковые алгоритмы, обращающиеся к каждой ячейке (и странице!) памяти всего один раз. А если обращение к некоторым страницам памяти происходит неоднократно, – имеет ли значение порядок их обработки или нет? На первый взгляд, если обрабатываемые страницы уже находятся в TLB, – шаг чтения данных никакого значения не имеет. А вот давайте проверим! Для этого добавим в нашу тестирующую программу Memory/list.step.c цикл for(i = 0; i <= BLOCK_SIZE; i += 4*K) x += *(int *)((int)p + i + 32), заставляющий систему спроецировать все страницы и загрузить их в TLB до начала замера времени исполнения. (Читателям достаточно лишь раскомментировать определение UNTLB). В результате получится следующее (см. рис. graph 11).
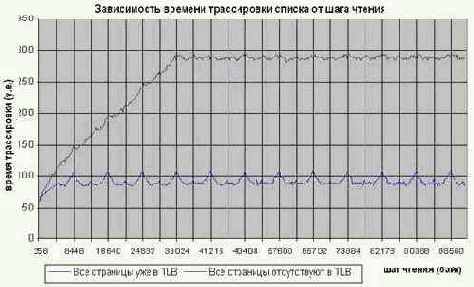
Рисунок 28 graph 11 График, иллюстрирующий время обработки блока данных в зависимости от шага чтения при отсутствии и присутствии страниц в TLB. Обратите внимание на "волнистость" нижней кривой. Это – прямое следствие регенерации DRAM банков оперативной памяти.
Смотри-ка, а ведь время трассировки списка и, правда, многократно уменьшилось! Зависимость скорости обработки от величины шага на первый взгляд как будто бы исчезла, но при внимательном изучении графика на нем все же обнаруживается мелкая "рябь". Строгая периодичность "волн" говорит нам о том, что это не ошибка эксперимента, а некая закономерность. Весь вопрос в том, – какая? Падение производительности на гребнях волны достигает ~30% и списывать эту величину на "мелкие брызги" побочных эффектов, – было бы с нашей стороны откровенной наглостью.
Характер кривой объясняется особенностями организации оперативной памяти. Как нам уже известно, время доступа к памяти непостоянно и зависит от множества факторов. Максимальная производительность достигается когда: а) запрашиваемые ячейки находятся в открытых страницах DRAM; б) ни страница, ни банк памяти в момент обращения к ним не находится на регенерации.
Исходя из пунктов а) и б) попробуйте ответить на вопрос: как изменяется время доступа к ячейкам памяти в зависимости от шага чтения?
Так – так – так… (глубоко затянувшись и откинувшись на спинку стула). Начнем с пункта а). Из самых общих рассуждений следует, что по мере увеличения шага время доступа будет пропорционально расти за счет более частого открытия страниц. Так будет продолжаться до тех пор, пока длина шага не достигнет длины одной DRAM-страницы (типичная длина которой 1, 2 и 4 Кб), после чего открытия страниц станут происходить при каждом доступе к ячейке и кривая, достигнув максимума насыщения, перейдет в горизонтальное положение. Попробуем проверить наше предположение на практике, запустив следующий тест (см. Memory/memory.hit.miss.c), поскольку масштаб графика graph 11 не очень-то подходит для точных измерений.
// шапка для Word'а
printf("STEP");
for(pg_size=STEP_SIZE;pg_size<=MAX_PG_SIZE;pg_size+=(STEP_SIZE*STEP_FACTOR))
printf("\t%d",pg_size);printf("\nTime");
// основной цикл, различные шаги чтения
for(pg_size=STEP_SIZE;pg_size<=MAX_PG_SIZE;pg_size+=(STEP_SIZE*STEP_FACTOR))
{
A_BEGIN(0) /* начало замера времени выполнения */
// цикл, читающий память с заданным шагом
// поскольку, количество физической памяти ограничено,
// а при большом шаге чтения все читаемые ячейки поместятся в кэше
// приходится хитрить и представлять память как кольцевой массив
// в общем, этот алгоритм нагляднее описывается кодом, чем словами
for (b=0;b<pg_size;b+=STEP_SIZE)
for(a=b;a<BLOCK_SIZE/sizeof(int);a+=(pg_size/sizeof(int)))
x+=p[a];
A_END(0) /* конец замера времени выполнения */
printf("\t%d",Ax_GET(0)); /* печать времени выполнения */
PRINT_PROGRESS(100*pg_size/MAX_PG_SIZE);
}
Листинг 17 [Memory/DRAM.wave.c] Фрагмент программы, предназначенной для детального изучения "волн" DRAM-памяти
Смотрите (см. рис. 0х29), – восходящая ветвь кривой действительно ведет себя в соответствии с нашими предположениями, но не достигает максимума насыщения, а переходит в чрезвычайно испещренную пиками и рытвинами местность. Время доступа к ячейкам с ростом шага меняется непрерывно, но график – к счастью! – обнаруживает строгую периодичность, что вселяет надежду на возможность его расшифровки. Собственно, это не график даже, а кладезь информации, раскрывающая секреты внутренней структуры и организации микросхем памяти. Итак, заправляемся пивом и начинаем…
Закон №1 (возьмите себе на заметку) где есть периодичность, там всегда есть структура. Значит, память, – это не просто длинная цепочка ячеек, а нечто более сложное и неоднородное. Да, мы знаем, что память состоит из страниц, но одного этого факта явно недостаточно для объяснения формы кривой. Требуется что-то еще… Не замешено ли здесь расслоение памяти на банки и их регенерация? Давайте прикинем. Время доступа к ячейке без регенерации занимает 2 (RAS to CAS Delay) + 2 (CAS Delay) + 1 + 1 + 1 == 7 тактов, а с регенерацией: 2 (RAS Precharge) + 2 (RAS to CAS Delay) + 2 (CAS Delay) + 1 + 1 + 1 == 9 тактов, что в 1.225 раз больше. Согласно графику 0x29 время обработки блока на "вершине" горы составляет 22.892.645 тактов, а у ее "подножия" – 18.610.240 тактов, что соответствует отношению в 1.23 раз. Цифры фантастическим образом сходятся! Значит, наше предположение на счет регенерации верно! (Точнее, как осторожные исследователи, мы должны сказать "скорее всего верно", но… это было бы слишком скучно)
Вообще-то, на этом можно было бы и остановится, поскольку закладываться на физическую организацию оперативной памяти столь же безрассудно, как и вкладывать свои ваучеры в МММ. С другой стороны: вполне можно выделить ряд рекомендаций, общих для всех или, по крайней мере, большинства моделей памяти. Особого прироста производительности их соблюдение, впрочем, не принесет, но вот избежать
более чем 20%-30% падения производительности – поможет.
Тонкая оптимизация для "гурманов" В первую очередь нас будет интересовать схема отображения физических ячеек памяти на адресное пространство процессора (см. "Отображение физических DRAM-адресов на логические"), а так же количество и размер банков, длина страниц и все остальные подробности.
Достаточно очевидно, что гребень волны соответствует той ситуации, когда каждое обращение к памяти попадает в регенерирующийся банк. Отсюда: расстояние между двумя соседними гребнями равно произведению длины одной DRAM страницы на количество банков (в нашем случае – 8 Кб), что удовлетворяет следующим комбинациям: 1 Кб (длина DRAM-страницы) x 8 (банков), 2 x 4, 4 x 8 и 8 x 1. Можно ли определить какой именно тип памяти используется в действительности? Да, можно и ключ к этому дает ширина склона "горы" (на рис. 29 она обозначена символом d). Легко доказать, что ширина склона "горы" в точности соответствует длине одной DRAM-страницы. Действительно, путь c – длина одной страницы, а N – количество банков. Тогда, расстояние между концом одной и началом другой страницы всякого банка равно (N-1) * c /* 1 */, соответственно, расстояние между двумя страницами одного банка равно Nc /* 2 */, а расстояние между началом одной и концом другой страниц – (N + 1) * c /* 3 */.
Ситуация /* 1 */ соответствует самому подножию горы, – если шаг чтения меньше чем (N ? 1) * c, то, независимо от смещения ячейки в странице, следующая запрашиваемая ячейка гарантированно не находится в том же самом банке. Но что произойдет, если шаг возрастет хотя бы на единицу? Правильно, при чтении последней ячейки одной DRAM-страницы, очередная ячейка придется на… следующую страницу того же самого банка! (Если не совсем понимаете, о чем идет речь, попробуйте изобразить это графически). Дальнейшее увеличение шага будет захватывать все больше и больше ячеек, вызывая неуклонное снижение производительности.
Так будет продолжаться до тех пор, пока шаг чтения не сравняется с /* 2 */, после чего начнется обратный процесс. Теперь, все больше и больше ячеек будут "вылетать" в страницы соседнего банка, уже готового к обработке запроса…
Отсюда: ширина склона "горы" равна N*c – (N ? 1)*c. Раскрываем скобки и получаем: N*c – N*c + c == c, что и требовалось доказать. Зная же c, вычислить N будет совсем не сложно: количество банков равно отношению расстояния между двумя пиками к ширине склона одной "горы", т.е. приведенный график соответствует четырех банковой памяти с длиной страницы в 2 Кб.
Бесспорно, эта методика весьма перспективна в плане создания тестирующей программы (надо же знать какое оборудование вам подсунули продавцы), но поможет ли она нам в оптимизации программ? Ввиду большого количества "разношерстных" моделей памяти, величина оптимального (неоптимального) шага чтения памяти на стадии разработки программы неизвестна
и должна определятся динамически на этапе исполнения, "затачиваясь" под конкретную аппаратную конфигурацию.
Причем, сказанное относится не только к трассировке списков и других ссылочных структур, но и к параллельной обработке нескольких потоков данных. Рассмотрим, например, такой код:
int *p1, int p2;
p1=malloc(BLOCK_SIZE*sizeof(int));
p2= malloc(BLOCK_SIZE*sizeof(int));
…
if (memcmp(p1,p2, BLOCK_SIZE*sizeof(int)) …
…
Листинг 18 Пример неоптимального программного кода, – оба блока памяти могут начинаться с одного и того же DRAM банка, вследствие чего их параллельная обработка окажется невозможна.
Как вы думаете: можно ли считать этот фрагмент программы оптимальным? А вот и нет! Ведь никто не гарантирует, что блоки памяти, возвращенные malloc-ом, не начинаются с одного и того же банка. Скорее, нам гарантированно обратное. Если размер блока превышает 512 Кб (а про обработку вот таких гигантских массивов памяти мы и говорим!), он не может быть размещен в куче и необходимую память приходится выделять с помощью win32 API?функции VirtualAlloc.
К несчастью, возвращаемый ей адрес всегда выравнивается на границу 64 Кб, т.е. величину, кратную любым разумным сочетаниям Nc. Т.е. попросту говоря, все выделяемые malloc-ом блоки памяти начинаются с одного и того же банка! А это не есть хорошо!!! Точнее – это просто кретинизм! Неужели разработчики системы проглядели такой ляп? Что ж, это не сложно проверить, – достаточно написать программку, выделяющую блоки памяти разного размера и анализирующую значения 11 и 12 битов (эти биты отвечают за выбор DRAM-банка).
#define N_ITER 9 // кол-во итераций
#define STEP_FACTOR (100*1024) // шаг приращения шага размера памяти
#define MAX_MEM_SIZE (1024*1024)
#define _one_bit 11 // эти биты отвечают...
#define _two_bit 12 // ...за выбор банка
#define MASK ((1<<_one_bit)+(1<<_two_bit))
#define zzz(a) (((int) malloc(a) & MASK) >> _one_bit)
main()
{
int a,b;
PRINT(_TEXT("= = = Определение номеров DRAM-банков = = =\n"));
PRINT_TITLE;
printf("BLOCK\n SIZE - - - n BANK - - -\n");
printf("----!----------------------------------------------------------\n");
for(a = STEP_FACTOR; a < MAX_MEM_SIZE; a += STEP_FACTOR)
{
printf("%04d:",a/1024);
for (b = 0; b < N_ITER; b++)
printf("\t%x",zzz(a));
printf("\n");
}
}
Листинг 19 [Memory/bank.malloc.c] Фрагмент программы, определяющий номера банков с которых начинаются блоки памяти, выделяемые функцией malloc
Результат ее работы будет следующим:
BLOCK
SIZE (Кб) - - - n BANK - - -
----!------------------------------------------------------------------
0100: 0 2 0 2 0 2 0 2 0
0200: 0 0 0 0 0 0 0 0 0
0300: 0 2 0 2 0 2 0 2 0
0400: 2 2 2 0 0 0 0 0 0
0500: 2 0 2 0 2 0 2 0 2
0600: 0 0 0 0 0 0 0 0 0
0700: 0 0 0 0 0 0 0 0 0
0800: 0 0 0 0 0 0 0 0 0
0900: 0 0 0 0 0 0 0 0 0
1000: 0 0 0 0 0 0 0 0 0
Смотрите, – до тех пор, пока размер выделяемых блоков не достиг 512 Кб, нам попадались как удачные, так и неудачные комбинации, но, начиная с 512 Кб, все выделенные блоки, действительно, начинаются с одного и того же банка.
Что же делать? Писать собственную реализацию malloc? Конечно же, нет! Достаточно динамически определив N и c, проверить соответствующие биты в адресах, возращенных malloc. И, если они вдруг окажутся равны, – увеличить любой из адресов на величину c (естественно, размер запрашиваемого блока необходимо заблаговременно увеличить на эту же самую величину). В результате мы теряем от 1- до 4 Кб, но получаем взамен, по крайней мере, 20%-30% выигрыш в производительности.
Это тот редкий случай, когда знание приемов "черной магии" позволяет совершенно непостижимым для окружающих способом увеличить быстродействие чужой программы, добавив в нее всего одну строку, даже без анализа исходных текстов. Маленькое лирическое отступление. Однажды поручили мне в порядке конкурсного задания оптимизацию одной программы, уже и без того оптимизированной – по понятиям заказчика – "по самые помидоры". Собственно, проблема заключалась в том, что львиная доля процессорного времени уходила не на вычисления, а на обмен с оперативной памятью, причем размер обрабатываемых данных был действительно сокращен до предела и Заказчик пребывал в абсолютной уверенности, что оптимизировать тут более нечего… Каково же было его удивление когда я прямо на его глазах, бегло пробежался контекстным поиском по исходным тестам и, даже не удосужившись запустить профилировщик, просто воткнул в нескольких местах код a'la p += 4*1024, после чего программа заработала приблизительно на треть быстрее.
Он (Заказчик) долго и недоверчиво спрашивал: уверен ли я, что это не случайность и под всяким ли железом и операционной системе это будет работать? Нет, не случайность. Уверен. Будет работать под любой OC семейства Windows и почти на любом железе: микросхемах памяти с организацией 2 x 4, 4 x 2, 4 x 2, 4 x 4, а на чипсетах серии Intel 815 (и других подобным им) вообще на всех
типах памяти. Эти чипсеты отображают 8- и 9-биты номера столбца на 25- и 26-биты линейного адреса, а вовсе не на 11- и 12-биты, как того следовало ожидать. Попросту говоря, программная длина DRAM-страниц на таких чипсетах всегда равна 2 Кб, потому на всех модулях памяти, имеющих по крайней мере четырех банковую организацию (а все модули емкостью от 64 и более мегабайт такую организацию и имеют), сдвиг указателя на 4 Кб гарантированно исключает попадание в тот же самый DRAM-банк.
Конечно, закладываться на такие особенности аппаратуры – дурной тон и в программах, рассчитанных на долговременное использование, настоятельно рекомендуется не лениться, а определять длину DRAM-страниц автоматически или, на худой конец, позволять изменять эту величину опционально.
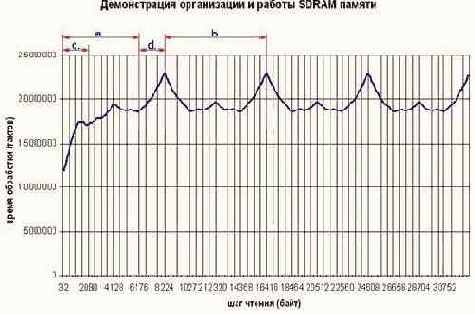
Рисунок 29 0x029 / graph 0x004 "Волны" памяти несут чрезвычайно богатую информацию о конструктивных особенностях используемых микросхем памяти. Вот только основные характеристики: а. – расстояние между концом одной и началом следующей DRAM-страницы того же самого DRAM-банка; b. – расстояние между началом одной и началом другой DRAM-страницы того же самого DRAM-банка (т.е. размер всех DRAM-банков); c. и d. – размер одной DRAM-страницы. Кол-во DRAM банков равно b/d