Планирование дистанции предвыборки
Поскольку, оперативная память – устройство медленное, загрузка кэш-линеек – дело долгое. Соответственно, предвыборку необходимо выполнять заблаговременно, с таким расчетом, чтобы, когда до обрабатываемых данных дойдет очередь, они уже находились в кэше.
При линейной обработке данных добиться этого очень просто, вот циклы – дело другое. Как быть, если время загрузки данных превышает продолжительность одной итерации? В примерах???2,4, приведенных выше, проблема решалась предвыборкой данных, обрабатываемых в следующей итерации цикла. Обратите внимание – именно следующей
итерации, а не через одну итерацию. Поэтому, лишь в первом проходе цикл исполняется неэффективно, а все последующие идут "на ура".
Как же это получается?! Весь если предвыборка успевает загружать данные за время выполнения предыдущей итерации, продолжительность загрузки не превышает продолжительности одной итерации, а раз так – зачем вообще потребовался этот сдвиг, ведь по идее данные должны успевать загружаться в течение текущего прохода цикла?
Ответ на вопрос кроется в механизме взаимодействия ядра процессора с подсистемой памяти. ### Подробно он рассматривался в первой части настоящей книги (см. "Устройство и принципы функционирования оперативной памяти. Взаимодействие памяти и процессора"), здесь же напомним читателю лишь основные моменты. ### Ввиду ограниченности объема журнальной статьи не будем останавливаться на этом подробно, а рассмотрим лишь основные моменты. В первую очередь нас будет интересовать поведение процессора при чтении ячеек памяти, отсутствующих в кэшах обоих уровней. Убедившись, что ни L1, ни в L2 кэше требуемой ячейки нет (и израсходовав на это один такт), процессор принимает решение получить недостающие данные из оперативной памяти. "Выплюнув" в адресную шину адрес ячейки, процессор, ценой еще нескольких тактов, передает его контроллеру памяти. Затем чипсет вычисляет номер столбца и номер строки ячейки, и смотрит: открыта ли соответствующая страница памяти или нет? Если страница действительно открыта, чипсет выставляет сигнал CAS и спустя 2-3 такта (в зависимости от величины задержки CAS, обусловленной качеством микросхемы памяти) на шине появляются долгожданные данные. (Если же требуемая строка закрыта, но максимально допустимое количество одновременно открытых строк еще не достигнуто, чипсет посылает микросхеме памяти сигнал RAS вместе с адресом строки и дает ей 2-3 такта на его "переваривание", затем посылается CAS и все происходит по сценарию описанному выше, в противном случае приходится терять еще такт на закрытие одной из страниц).
Контроллер памяти "проглатывает" первую порцию данных за один такт и с началом следующего такта передает ее заждавшемуся процессору, параллельно с этим "выдаивая" из микросхемы памяти вторую. Количество порций данных, загружаемых за один шинный цикл обращения к памяти, на разных процессорах различно и определяется размером линеек кэша второго уровня. В частности, P-II и K6, с 32-байтными кэш-линейками заполняют их четырьмя 64-битных порциями данных. Легко подсчитать, что полное время доступа к памяти требует от 10 до 12 тактов системной шины, но только 4 из них уходят на непосредственную передачу данных, а все остальное время шина свободна.
Однако если адрес следующей обрабатываемой ячейки известен заранее, процессор может отправить контроллеру очередной запрос, не дожидаясь завершения предыдущего. Конвейеризация позволяет скрыть латентность (начальную задержку) памяти, сократив время доступа к памяти с 10(12) тактов до 4 (см. рис 0х27). Правда, чтение первой ячейки будет по-прежнему требовать 10-12 тактов, но при циклической обработке данных этой задержкой можно пренебречь. Вот и ответ на вопрос – почему для эффективной предвыборки данных потребовался сдвиг на одну итерацию. Это необходимо для компенсации времени латентности (Tl), которая в данном случае существенно превосходит полезное время передачи данных (Tb).
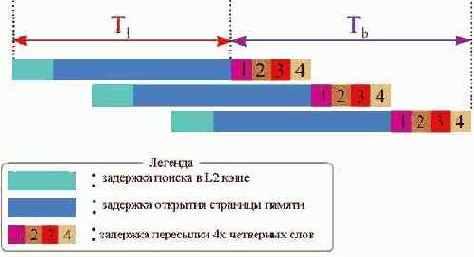
Рисунок 42 0х27 Демонстрация конвейеризации обмена с памятью.
Время выполнения цикла без использования предвыборки. В отсутствии предвыборки время выполнения цикла определяется суммой времени выполнения вычислительных инструкций цикла (Tc), времени латентности (Tl) и времени загрузки данных (Tb). Причем, во время выполнения вычислений системная шина простаивает, а во время загрузки данных, наоборот, вычислительный конвейер простаивает, а шина – работает. Причем, время доступа к памяти определяется не пропускной способностью шины, а латентностью подсистемы памяти. Шина же в лучшем случае нагружена на 15%-20% (см. рис. 0х028)
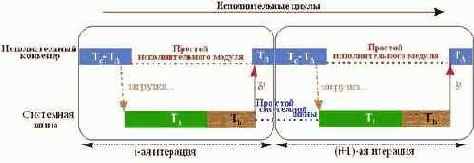
Рисунок 43 0х28 Исполнение цикла без использования предвыборки.
Время выполнения цикла в случае Tc>=Tl+Tb. Если время выполнения вычислительных инструкций цикла равно или превышает сумму времен латентности памяти и загрузки данных, упреждающая предвыборка эффективно распараллеливает работу системной шины с работой вычислительного конвейера (см. рис. 0х029).
Задержки доступа к памяти полностью маскируются, и время выполнения цикла определяется исключительно объемом вычислений, при этом производительность увеличивается в раз, т.е. в лучшем случае (при Tc=Tl+Tc) время выполнения цикла сокращает вдвое.
Минимальная дистанция предвыборки равна одной итерации, однако, если программа попадет на быстрый компьютер с медленной памятью (что типично для офисных и домашних компьютеров), запрошенные ячейки не успеют загрузиться за время выполнения предыдущей итераций. Это приведет к образованию "затора" на шине, вынужденному простою процессора и, как следствие, - тормозам.
Наилучший выход из ситуации – увеличить дистанцию предвыборки до двух-трех итераций. Да, мы теряем несколько первых проходов цикла, но при большом числе итераций, два-три прохода – это "капля в море"!
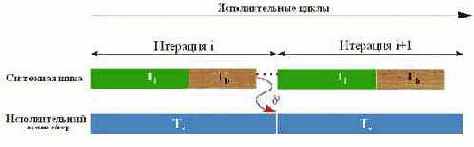
Рисунок 44 0х29 Исполнение цикла Tc>=Tl+Tb с дистанцией предвыборки в одну итерацию. Стрелкой с символом df показана зависимость по данным.
Время выполнения цикла в случае Tl+Tb > Tc> Tb. Если полное время доступа к памяти (т.е. сумма времени латентности и времени загрузки данных) превышает время выполнения вычислительных инструкций (Tc), но время выполнения вычислений в свою очередь превышает время загрузки данных, эффективное распараллеливание по-прежнему возможно! Необходимо лишь конвейеризовать запросы на загрузку данных, запрашивая очередную порцию данных до получения предыдущей. Это достигается увеличением дистанции предвыборки на несколько итераций, минимальное количество которых определяется по формуле:
(1),
где psd - Prefetch Scheduling Distance, – планируемая дистанция предвыборки, измеряемая в количестве итераций. Точно так, как и в предыдущем примере, в данном случае дистанцию предвыборки лучше взять с запасом, чем недобрать.
В худшем случае производительность увеличивается в два раза, а в среднем – в 4-5 раз (поскольку, типичная латентность памяти порядка 10 тактов, а время загрузки данных – 4 такта, то при Tc = Tb
получаем: ), причем загрузка системной шины достигает 80%-90% (в идеале – 100%). Великолепный результат, не так ли?
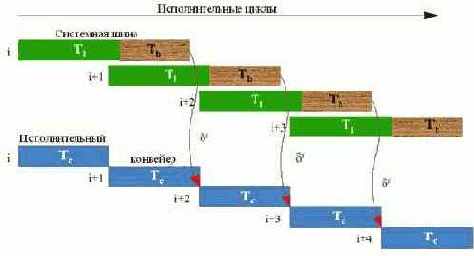
Рисунок 45 0х30 Исполнение цикла Tl+Tb > Tc> Tb. с дистанцией предвыборки в две итерации. Стрелкой с символом df показана зависимость по данным.
Время выполнения цикла в случае Tb > Tc. Наконец, если время загрузки данных (Tb) превышает время выполнения вычислительных инструкций цикла, полный параллелизм становится невозможен в принципе, – раз загрузка превышает продолжительность одной итерации, простой вычислительного конвейера неизбежен и никакая предвыборка тут не поможет. Тем не менее, предвыборка все же будет полезной, поскольку позволяет маскировать латентность памяти, что дает двух-трех кратный прирост производительности. Согласитесь – величина не малая. Оптимальная дистанция предвыборки определяется по формуле: (2).
Поскольку время выполнения цикла определяется исключительно скоростью загрузки данных (т.е. фактически частотой системной шины, загрузка которой в этом случае достигает 100%), излишне усердствовать над оптимизацией кода нет никакого смысла. Такая ситуация имеет место в частности, при копировании или сравнении блоков памяти. (Хотя, о оптимизация копирования – разговор особый. см. "Секреты копирования памяти или практическое применение новых команд процессоров Pentium-III и Pentium-4").
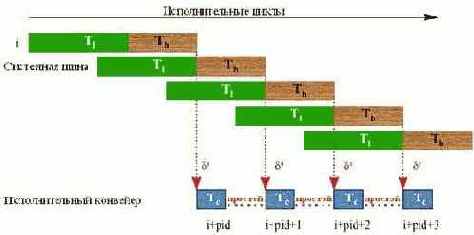
Рисунок 46 0х31 Исполнение цикла Tb > Tc. с дистанцией предвыборки в три итерации. Стрелкой с символом df показана зависимость по данным.
Практическое планирование предвыборки. Для вычисления оптимальной дистанции предвыборки необходимо знать: величину латентности памяти (Tl), время загрузки данных (Tb) и продолжительность выполнения одной итерации цикла (Tc). Поскольку, все три аргумента аппаратно–зависимы, приходится либо динамически
определять их значения в ходе выполнения программы, либо статически вычислять нижний предел дистанции предвыборки. Рассмотрим оба алгоритма подробнее.
Динамическое определение дает наивысший прирост производительности и достаточно просто реализуется. Один из возможных алгоритмов выглядит так: замеряв время выполнения первой итерации цикла (это можно сделать, например, посредством инструкции RDTSC), мы получаем сумму Tc+Tl+Tb. Затем, повторным выполнением этой же итерации, мы находим величину Tc (т.к. данные уже находятся в кэше время доступа к ним пренебрежительно мало). Разность этих двух величин даст сумму Tl+Tb, которой, вкупе с "чистой" Tc, вполне достаточно для вычисления формулы (???1).
Правда, определить "чистое" время Tb, необходимое для формулы (???2), таким способом довольно затруднительно, и лучше прибегнуть к алгоритму "вилки", суть которого заключается в следующем. Перебирая различные дистанции предвыборки и сравнения продолжительность соответствующих им итераций цикла, мы всего за несколько проходов найдем наиболее оптимальное значение, да не просто оптимальное, а самое-самое оптимальное, т.к. наилучшая дистанция предвыборки зачастую изменяется в процессе выполнения цикла. Особенно это характерно для разветвленных циклов, обрабатывающих неоднородные данные. К тому же динамический алгоритм определения дистанции предвыборки автоматически адоптируется под новые, еще не знакомые ему модели процессоров, в то время как статический анализ бессилен предвидеть их характеристики (Никто случайно не знает вычислительную скорость P-7?)
Статическое определение. В программах, рассчитанных на долговременное использование, статическое определение дистанции предвыборки нецелесообразно.
Никто не знает: какими будут процессоры через несколько лет, да и в настоящее время их характеристики повержены значительному разбросу. Если у CELERON-800 отношение частоты системной шины к частоте ядра равно 1:8, то у Pentium-4 1.300 оно лишь чуть-чуть не дотягивает 1:3. Вследствие этого соотношение у них будет сильно не одинаковым, и дистанция предвыборки, оптимальная для CELERON'а, окажется слишком малой для P-4, которому придется проставить, томительно ожидания загрузки очередной порции данных, в результате чего переход с CELETON на P-4 практически не увеличит производительности такой программы.
Поэтому, дистанцию предвыборки всегда планируйте с приличным запасом, по крайней мере, на 3-4 итерации больше необходимого минимума. Минимально необходимая дистанция предвыборки упрощенно вычисляется так:
(4)
где:
psd - Дистанция предвыборки (итераций цикла)
- Латентность памяти (тактов)
- Время загрузки кэш-строки (тактов)
- Количество предвыбираемых и сбрасываемых кэш-линий (штук)
CPI - Время выполнения одной инструкции (такты)
- Количество инструкций в одной итерации цикла (штуки)
В этой формуле почти все члены – неизвестные. Латентность памяти варьируется в очень широких пределах, поскольку определяется и типом самой памяти (SDRAM, DDR SDRAM, Rambus), и качеством чипов памяти (т.е. латентностью RAS и CAS), и "продвинутостью" чипсета, и, наконец, отношением частоты системной шины к частоте ядра процессора. Время загрузки кэш-строк пропорционально длине этих самых строк, которая составляет 32, 64 или 128 байт в зависимости от модели процессора (причем имеется ярко выраженная тенденция увеличения длины кэш-строк производителями).
Среднее время выполнения одной инструкции – вообще абстрактная величина, вроде среднего дохода граждан. Наряду с командами по трое сходящими с конвейера за один такт, некоторые (между прочим, достаточно многие) инструкции требуют десятков, а то и сотен тактов для своего выполнения! (В частности, целочисленное деление – не самая редкая операция, правда? – занимает от 50 до 70 тактов).
Таким образом, статическое планирование предвыборки в чем-то сродни гаданию на кофейной гуще. Но почему бы действительно не погадать? Intel приводит следующую эвристическую формулу, явно оговаривая ее ограниченность:
(5)
Подсчет количества инструкций в цикле () – очень интересный момент. Даже реализуя критические циклы на ассемблере (что для сегодняшнего дня вообще-то редкость), программист не может быть абсолютно уверен, что транслятор не впихнул туда чего-нибудь по собственной инициативе (например, NOP'ов для выравнивания). Что же тогда говорить о языках высокого уровня! Количество инструкций достоверно определяется лишь ручным их подсчетом в ассемблерном листинге (большинство компиляторов такие листинги генерировать умеют), однако, во-первых, это утомительное занятие придется проводить при всяком изменении текста программы. Во-вторых, если в цикле вызываются внешние функции (например, API-функции операционной системы) потребуется либо раздобыть исходные тексты ОС, либо дизассемблировать соответствующую функцию (но исходные тексты в большинстве случаев недоступны, а дизассемблер далеко не каждый умеет держать в руках). Наконец, в-третьих, полученный таким трудом результат все равно окажется неверным и ничуть не уступающим в точности киданию кости.
К счастью, интервал оптимальной дистанции предвыборки очень широк – даже увеличение минимального значения на порядок (!) в большинстве случаев снижает производительность не более чем на 10%-15% (а на многократно выполняющихся циклах – и того меньше). Поэтому, если скорость выполнения кода некритична, – динамическое определение дистанции предвыборки допустимо заменить статическим планированием, увеличив предвычисленный результат в несколько раз.
Хорошая идея – позволить пользователю задавать дистанцию предвыборки опционально. Чтобы не загромождать интерфейс и не смущать неопытных пользователей эти настойки можно запихнуть в реестр.