Особенности обработки двумерных массивов
Техника параллельной загрузки данных (подробно рассмотренная в первой части настоящей книги) весьма эффективный способ… отправить свою программу на кладбище. Подсистема памяти не так проста как кажется, и один неосторожный шаг способен разнести всю оптимизацию к черту. Но довольно лирики! Переходим к делу.
Допустим, у нас имеется здоровенный двухмерный массив, сумму ячеек которого и требуется подсчитать. Для определенности возьмем матрицу 512х512, состоящую из переменных типа int. Двухмерность массива порождает буриданову проблему: как вести подсчет– по строкам или по столбцам?
Подсчет по строкам фактически сводится к последовательному чтению памяти, а это (как мы помним) далеко не лучший способ обработки данных. Куда заманчивее читать массив по столбцам. Если ширина матрицы превышает длину пакетного цикла обмена, запросы к памяти генерируются при каждом
кэш-промахе (см. "Часть I.Оптимизация работы с памятью. Параллельная обработка данных"). Единственное условие – произведение столбцов на размер кэш-линии не должно превышать емкости кэш-памяти первого уровня.
Соблюдается ли это условие в данном случае? На первый взгляд как будто бы соблюдается. Смотрите: на P-III размер кэш-линеек составляет 32 байта, а размер кэш-памяти первого уровня – 16 Кб. В то же время: 512 x 32 = 16.384. Совпадают ли цифры? Совпадают! Хорошо, возьмем, например, AMD Athlon, имеющий 64 Кб кэш при длине линеек в 64 байт. Умножаем 512 на 64 – получаем 32 Кб, что с лихвой должно вместится в кэш. Но вместится ли? Сейчас проверим! Запустим на выполнение следующий пример:
#define N_ROW (512)
#define N_COL (512) // неоптимальное колю строк матр.
// поскольку оно кратно размеру
// кэш-банка и кэш используется
// _не_ полностью
/*----------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНАЯ ОБРАБОТКА МАССИВА ПО СТОЛБЦАМ
*
----------------------------------------------------------------------------*/
int FOR_COL(int (*foo)[N_COL])
{
int x, y;
int z = 0;
for (x = 0;x < N_ROW; x++)
{
for (y = 0; y < N_COL; y++)
z += foo[x][y];
}
return z;
}
/*----------------------------------------------------------------------------
*
* ПОСЛЕДОВАТЕЛЬНАЯ ОБРАБОТКА МАССИВА ПО СТРОКАМ
*
----------------------------------------------------------------------------*/
int FOR_ROW(int (*foo)[N_COL])
{
int x, y;
int z = 0;
for (x = 0; x < N_COL; x++)
{
// внимание: если высота матрицы кратна размеру кэш-банка, то
// вследствии ограниченной ассоацитивности кэша его эффективная
// емкость значительно снизится и кэш-памяти может по просту
// не хватить, что приведет к постоянным промахам!
for (y = 0; y < N_ROW; y++)
z += foo[y][x];
}
return z;
}
Листинг 12 [Cache/column.big.c] Пример, демонстрирующий особенности обработки больших двухмерных массивов
Да как бы ни так! Мы совсем забыли про ассоциативность – поскольку, адреса читаемых ячеек кратны 4096, всего лишь четыре ячейки могут одновременно находится в кэше, но никак не 1024! Даже емкости кэша второго уровня для этих целей окажется недостаточно! Допустим, мы имеем, четырех ассоциативный 128 Кб L2-кэш. Каждый его банк способен хранить CACHE.SIZE/WAY/STEP.SIZE = 131.072/4/4096 == 32 таких ячеек. Следовательно, четыре банка разместят 32*4 = 128 ячеек. А у нас их аж 1024… Облом-с!
Сверхоперативная память будет крутиться полностью вхолостую, а величина кэш-промахов достигнет даже не 100%, а… 800% на P-II/P-III и 1.600% на AMD Athlon! Действительно, ведь в силу пакетного обмена, кэш-строки заполняются целиком, но только малая их часть оказывается реально востребована! В результате, данный код будет исполняется очень медленно.
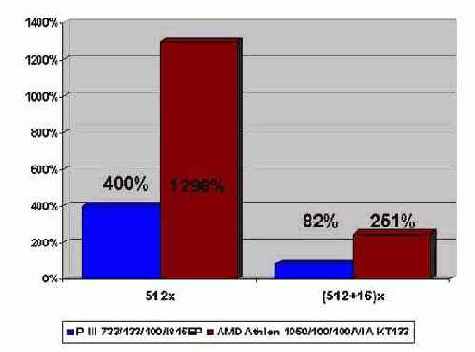
Рисунок 31 graph 0x011 Зависимость времени обработки двухмерных массивов в зависимости от шага чтения.
Поскольку, обмен с кэшем и основной оперативной памятью осуществляется не отдельными ячейками, а пакетами достигающими в длину от 32 до 128 байт, при последовательной обработке ячеек время доступа к ним оказывается крайне неоднородным. Задержки возникают лишь при чтении первой ячейки пакета, а остальные ячейки пакета обрабатываются практически мгновенно.
Из этого в частности следует, что большие многомерные массивы (т.е. не умещающиеся в кэш-памяти первого, а тем более второго уровней) выгоднее обрабатывать не по столбцам, а по строкам. Массивы, целиком влезающие в кэш, можно обрабатывать как угодно – от этого хуже не будет.
На первый взгляд, программа column.big.c переставляет собой пример чрезвычайно высоко оптимизированного кода. Благодаря величие своего шага, первый проход цикла for y инициирует параллельную загрузку ячеек из основной оперативной памяти (или кэша второго уровня). Поскольку, размер обрабатываемых данных составляет всего лишь 1024*CACHE_LINE_SIZE == 32 Кб (что целиком умещается в кэш первого или на худой конец второго уровня), – может показаться, что последующие итерации цикла будут обрабатываться практически мгновенно, – ведь данные уже в кэше, а не в памяти!
Чтобы решить проблему, программу следует реорганизовать так:
int x,y,z;
int foo[1024][1024];
for (x=0;x<1024;x++)
{
for (y=0; y<1024;y++)
{
z=foo[x][y];
}
}
Листинг 13
Обрабатывая цикл не по столбцам, а по строкам, мы избавляемся от кэш-конфликтов и снижаем процент кэш-промахов до разумного минимума. Если хотите – мы даже можем рассчитать его поточнее. Несмотря на то, что массив foo, занимая 1024x1024x4 = 4 Мб памяти, намного превосходит и кэш первого, и кэш второго уровня, мы имеем всего лишь 12.5% промахов на P-II/P-III, а AMD Athlon и вовсе обходимся пактически без промахов– 6.25%! Согласитесь, что 6.25% это совсем не тоже самое, что и 1.600%!
Вот такая она разница между строками и столбцами!
В кэше второго уровня ячейка foo[1][0] так же имеет немного шансов сохранится. Пускай, емкости L2-кэша хватает с лихвой, но в многозадачной системе этот кэш приходится делить между множеством приложений – поскольку, первый проход цикла растянется на десятки тысяч тактов процессора, в течение этого времени не раз и не два произойдет переключение контекста и управление будет передано другим задачам. Если хотя бы одна из них интенсивно работает с памятью она может затереть таким трудом загруженные в L2-кэш строки массива foo, и – весь труд насмарку!
Поскольку, величина шага цикла for y превышает размер пакетного цикла обмена с памятью, в осуществляется параллельная загрузка ячеек
Смотрите, как все происходит: при попытке обращения к ячейке foo[0][0] кэш-контроллер, выяснив, что в кэше первого уровня она отсутствует, обращается к кэшу второго уровня. Там этой ячейки, скорее всего, тоже нет и приходится загружать полную 32-байтную строку из оперативной памяти, на что расходуется десятки тактов процессора.
Следующая ячейка – foo[1][0] – расположенная в соседней строке массива, отстоит от только считанной ячейки на 1024x4 байт, что много больше длины 32-байтной кэш-линии, поэтому она вновь загружается из оперативной памяти…
Наконец, первая колонка полностью обработана и наступает черед второй. Ячейки foo[1][0] уже не содержится в кэше. Почему? Ведь мы прочли всего четыре килобайта (1.024х4 = 4.096), что много меньше емкости L1-кэша? Если же реорганизовать цикл, читая его вот так: z=foo[x][y] скорость обработки многократно возрастет! Действительно, задержка при обращении к ячейке foo[0][0] компенсируется тем, что последующие восемь ячеек будут прочитаны практически мгновенно! Аналогично – foo[0][4] вызывает задержку на время подрузки данных из оперативной памяти, но каждая из последующих ячеек foo[0][5] foo[0][6] … foo[0][12] читается за один такт! В результате мы получаем практически семикратное ускорение – неплохо, правда?