Оптимизация ссылочных структур данных
Итак, если мы не хотим, чтобы наша программа ползала со скоростью черепахи в летний полдень и на полную использовала преимущества высокопроизводительной DDR- и DRRAM памяти, – следует обязательно устранить зависимость по данным. Как это сделать?
Вот скажем, графический файл в формате BMP, действительно, можно обрабатывать и параллельно, поскольку он представляет собой однородный массив данных фиксированного размера. Совсем иная ситуация складывается с двоичными деревьями, списками и прочими ссылочными структурами, хранящими разнородные данные.
Расщепление списков (деревьев). Рассмотрим список, "связывающий" пару десятков мегабайт текстовых строк переменной длины. Как оптимизировать прохождение по списку, если адрес следующего элемента заранее неизвестен, а список к тому же сильно фрагментирован? Первое, что приходит на ум: разбить один список на несколько независимых списков, обработка которых осуществляется параллельно. Остается выяснить: какая именно стратегия разбиения наиболее оптимальна. В этом нам поможет следующая тестовая программа, последовательно прогоняющая списки с различной степенью дробления (1:1, 1:2, 1:4, 1:6 и 1:8). Ниже, по соображениям экономии бумажного пространства, приведен лишь фрагмент, реализующий комбинации 1:1 и 1:2. Остальные же степени дробления реализуются полностью аналогично.
#define BLOCK_SIZE (12*M) // размер обрабатываемого блока
struct MYLIST{ // элемент списка
struct MYLIST *next;
int val;
};
#define N_ELEM (BLOCK_SIZE/sizeof(struct MYLIST))
/* -----------------------------------------------------------------------
*
* обработка одного списка
*
----------------------------------------------------------------------- */
// инициализация
for (a = 0; a < N_ELEM; a++)
{
one_list[a].next = one_list + a + 1;
one_list[a].val = a;
} one_list[N_ELEM-1].next = 0;
// трассировка
p = one_list;
while(p = p[0].next);
/* -----------------------------------------------------------------------
*
* обработка двух расщепленных списков
*
----------------------------------------------------------------------- */
// инициализация
for (a = 0; a < N_ELEM/2; a++)
{
spl_list_1[a].next = spl_list_1 + a + 1;
spl_list_1[a].val = a;
spl_list_2[a].next = spl_list_2 + a + 1;
spl_list_2[a].val = a;
} spl_list_1[N_ELEM/2-1].next = 0;
spl_list_2[N_ELEM/2-1].next = 0;
// трассировка
p1 = spl_list_1; p2 = spl_list_2;
while((p1 = p1[0].next) && (p2 = p2[0].next));
// внимание! Данный способ трассировки предполагает, что оба списки
// равны по количеству элементов, в противном случае потребуется
// слегка доработать код, например, так:
// while(p1 || p2)
// {
// if (p1) p1 = p1[0].next;
// if (p2) p2 = p2[0].next;
// }
// однако это сделает его менее наглядным, поэтому в книге приводится
// первый вариант
Листинг 11 [Memory/list.splint.c] Фрагмент программы, определяющий оптимальную стратегию расщепления списков
На P-III 733/133/100/I815EP заметна ярко выраженная тенденция уменьшения времени прохождения списков, по мере приближения степени дробления к четырем. При этом быстродействие программы возрастает более чем в полтора раза (точнее – в 1,6 раз)! Дальнейшее увеличение степени дробления лишь ухудшает результат (правда незначительно). Причина в том, что при параллельной обработке более чем четырех потоков данных происходят постоянные открытия/закрытия DRAM-страниц, "съедающие" тем самым весь выигрыш от параллелизма (подробнее см. "Планирование потоков данных").
На AMD Athlon 1050/100/100/VIA KT133 ситуация совсем иная. Поскольку, и сам процессор Athlon, и чипсет VIA KT133 в первую очередь оптимизирован для работы с одним потоком данных, параллельная обработка расщепленных списков ощутимо снижает производительность.
Впрочем, расщепление одного списка на два все-таки дает незначительный выигрыш в производительности. Однако, наиболее оптимальна стратегия расщепления отнюдь не на два, и даже не на четыре, а… на шесть списков. Именно шесть списков обеспечивают наилучший компромисс при оптимизации программы сразу под несколько процессоров.
Разумеется, описанный прием не ограничивается одними списками. Ничуть не менее эффективно расщепление двоичных деревьев и других структур данных, в том числе и не ссылочных.
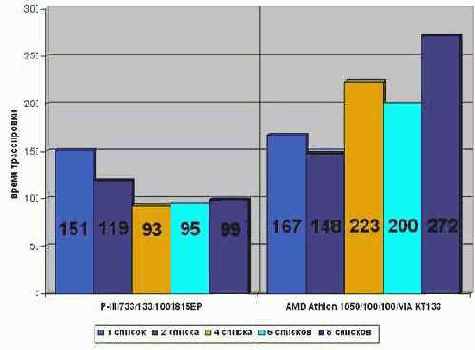
Листинг 12 graph 20 Зависимость времени обработки данных от степени расщепления списков. Как видно, наилучшая стратегия заключается в шестикратном расщеплении списков. Это обеспечивает наилучший компромисс для обоих процессоров
Быстрое добавление элементов. Чтобы при добавлении нового элемента в конец списка не трассировать весь список целиком, сохраняйте в специальном после ссылку на последний элемент списка. Это многократно увеличит производительность программы, под час больше чем на один порядок (а то и на два-три).
Подробнее об этом см. "Оптимизация строковых штатных Си-функций". Какое отношение имеют строки к спискам? Да самое непосредственное! Ведь строка это одна из разновидностей вырожденного списка, не сохраняющего ссылку на следующий элемент, а принудительно располагающая их в памяти так, чтобы они строго следовали один за другим.