Оптимизация блочных алгоритмов
Если с потоковыми алгоритмами все было предельно просто (хотя и не без тонкостей), то оптимизация блочных алгоритмов – вещь сама по себе нетривиальная. Если потоковая обработка данных предполагает, что данные запрашиваются последовательно и ничего не стоит организовать оптимальную (с точки зрения подсистемы памяти) трансляцию виртуальных адресов, то блочные алгоритмы могут в хаотичном порядке запрашивать любые ячейки в границах отведенного им блока. До тех пор, пока размер блока не превосходит эти пресловутые (N? 1)c – т.е. составляет порядка 4х-6ти килобайт, – никаких проблем не возникает, особенно если разрядность обрабатываемых данных сопоставима с величиной пакетного цикла обмена с память. В противном случае, возникают штрафные задержки при попадании в регенерирующиеся DRAM-банки, плюс издержки от упреждающего чтения данных к которым никто не обращается.
В идеале следовало бы посоветовать сократить размер блоков до нескольких килобайт, но – увы – такое решение не всегда возможно. Что ж, тогда придется прибегать к механизму виртуализации адресов. Пусть слово "виртуальный" не вводит вас в заблуждение относительно механизма реализации такого приема. Для этого вовсе не обязательно иметь наивысшие привилегии и доступ к системным таблицам. Виртуальную трансляцию вполне можно организовать и программным способом, один из которых мы уже рассмотрели выше при оптимизации потоковых алгоритмов.
К сожалению, эта тема не имеет прямого отношения к подсистеме оперативной памяти, и не может быть подробно рассмотрена в рамках этой книги. Давайте отложим этот вопрос по крайней мере до третьего тома.
Спекулятивная загрузка данных Алгоритм спекулятивной загрузки данных родился в те незапамятные времена, когда вычислительными залами владели "динозавры", а роль внешней памяти выполняла до ужаса тормозная магнитная лента. Первые программы работали приблизительно так: ЗАГРУЗИТЬ БЛОК ДАННЫХ С ЛЕНТЫ, ОБРАБОТАТЬ ДАННЫЕ, ПОВТОРИТЬ. Во время загрузки данных бобины с лентой бешено вращались, а на время вычислений покорно останавливались.
На обывателя это зрелище, действительно, действовало неотразимо, но для достижения наибольшей производительности ленточный накопитель должен работать не урывками, а непрерывно.
История не сохранила имя первого человека, которого осенила блестящая мысль: совместить обработку данных с загрузкой следующего блока. Если время выполнения не оптимизированной программы в общем случае равно: T = N*(Ttype + Tdp), где Type – время загрузки блока данных с ленты, Tdp
– время обработки блока, а N – количество блоков, то оптимизированный алгоритм может быть выполнен за: Toptimize = N*(max((Ttype + Tdp))).
Максимальный выигрыш достигается в том случае, когда время загрузки данных с ленты в точности равно времени вычислений. Как нетрудно подсчитать: T/Toptimize = N*(Ttype + Tdp)/ N*Ttype
== 2, т.е. время обработки сокращается в два раза.
И хотя бобины магнитной ленты уже давно вышли из употребления, – они до сих пор готовы преподнести всем нам хороший урок. Задумайтесь: как работает подавляющее большинство современных блочных алгоритмов? Какую программу ни возьми, всюду встречаешь сценарий: "загрузить – обработать – повторить". Пускай, быстродействие оперативной памяти не идет ни в какое сравнение со скоростью магнитной ленты, но ведь и тактовая частота процессоров не стоит на месте!
Простое смешивание команд загрузки содержимого ячеек памяти с вычислительными инструкциями (подробнее см. "Группировка вычислений с доступом к памяти") еще не обеспечивает их параллельного выполнения, – ведь вычислительные инструкции начинают выполняться только после окончания загрузки обрабатываемых данных!
Вспоминая сценарий работы с лентой, давайте усовершенствуем стратегию загрузки данных, обращаясь к следующему обрабатываемому блоку задолго до того, как он будет реально востребован. Этим мы устраним зависимость между командами загрузки и обработки данных, благодаря чему они смогут выполнятся параллельно, и, если время обработки данных не превышает времени их загрузки (как часто и бывает), обмен с памятью станет происходить непрерывно, вплотную приближаясь к ее максимальной пропускной способности. (см.
так же "Параллельная загрузка данных").
Рассмотрим следующий пример:
/*--------------------------------------------------------------------
не оптимизированный вариант
------------------------------------------------------------------- */
for(a = 0; a < BLOCK_SIZE; a += 32)
{
// загружаем ячейки
x += (*(int *)((int ) p + a)); // ß эта команда блокирует все остальные
x += (*(int *)((int ) p + a + 4));
x += (*(int *)((int ) p + a + 8));
x += (*(int *)((int ) p + a + 12));
x += (*(int *)((int ) p + a + 16));
x += (*(int *)((int ) p + a + 20));
x += (*(int *)((int ) p + a + 24));
x += (*(int *)((int ) p + a + 28));
// выполняем некоторые вычисления
x += a/x/666;
}
Листинг 42 Типовой не оптимизированный алгоритм обработки данных
Основной его недостаток заключается в том, что вычислительная процедура "x += a/x/666" вынуждена дожидаться выполнения всех предыдущих команд, а они в свою очередь вынуждены дожидаться окончания загрузки требуемых данных из памяти. Т.е. первая строка цикла "x+=*(int*)((int)p + a)" блокирует все остальные (а еще говорят, что семеро одного не ждут).
Можно ли устранить такую зависимость по данным? Да, можно. Достаточно, например, загружать данные со сдвигом на одну или несколько итераций (подробнее о вычислении предпочтительной величины сдвига см. "Кэш. Предвыборка"). Образно говоря мы как бы смещаем команды загрузки данных относительно инструкций их обработки. (см. рис. 43).
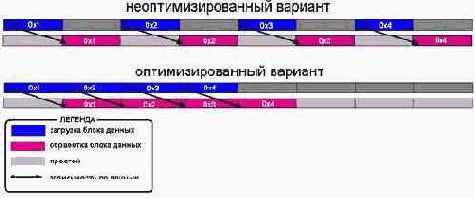
Рисунок 53 0х43 Устранение зависимости по данным путем упреждающей загрузки следующего обрабатываемого блока
В результате этого мы получаем приблизительно следующий код (обратите внимание, исходный текст программы практически не изменен!):
/*--------------------------------------------------------------------
оптимизированный вариант
со спекулятивной загрузкой
------------------------------------------------------------------- */
// загружаем первую порцию данных
x += (*(int *)((int) p + a));
for(a = 0; a < BLOCK_SIZE; a += 32)
{
// упреждающая загрузка очередной порции данных
y = (*(int *)((int) p + a + 32)); // ß ***
// обрабатываем ранее загруженные ячейки
x += (*(int *)((int) p + a + 4));
x += (*(int *)((int) p + a + 8));
x += (*(int *)((int) p + a + 12));
x += (*(int *)((int) p + a + 16));
x += (*(int *)((int) p + a + 20));
x += (*(int *)((int) p + a + 24));
x += (*(int *)((int) p + a + 28));
// выполняем некоторые вычисления
x += a/x/666;
// востребуем упреждено - загруженные данные
x += y;
}
Листинг 43 [Memory/Speculative.read.c] Фрагмент программы, демонстрирующий эффективность использования спекулятивной загрузки данных
На P-III/133/100/I815EP такой несложный трюк уменьшает время обработки данного цикла приблизительно на ~25%.
Почему всего лишь на четверть, а не на половину, как это следует из рис. 43? Причина в том, что команда "x += a/x/666" выполняется вдвое быстрее, чем загрузка следующего блока данных, потому и

Рисунок 54 Univac Компьютер UNIVAC с ленточным накопителем (слева) и женщиной-оператором (справа)