Балансировка логического древа
Оператор множественного выбора switch очень популярен среди программистов (особенно, разработчиков Windows-приложений). Число его ветвей может быть очень велико и их линейная обработка крайне непроизводительна.
В некоторых (хотя и редких) случаях, операторы множественного выбора содержат сотни (а то и тысячи) наборов значений, и если решать задачу сравнения "в лоб", то высота логического дерева окажется гигантской до неприличия, а его прохождение займет весьма длительное время, что не лучшим образом скажется на производительности программы.
Но, задумайтесь: чем собственно занимается оператор switch? Если отвлечься от устоявшейся идиомы "оператор SWITCH дает специальный способ выбора одного из многих вариантов, который заключается в проверке совпадения значения данного выражения с одной из заданных констант в соответствующем ветвлении", то можно сказать, что switch – оператор поиска соответствующего значения. В таком случае линейное switch - дерево представляет собой тривиальный алгоритм последовательного поиска – самый неэффективный алгоритм из всех.
Пусть, например, исходный текст программы выглядел так:
switch (a)
{
case 98 : …;
case 4 : …;
case 3 : …;
case 9 : …;
case 22 : …;
case 0 : …;
case 11 : …;
case 666: …;
case 096: …;
case 777: …;
case 7 : …;
}
Тогда соответствующее ему не оптимизированное логическое дерево будет достигать в высоту одиннадцати гнезд (см. рис. 1 слева). Причем, на левой ветке корневого гнезда окажется аж десять других гнезд, а на правой – вообще ни одного (только соответствующий ему case - обработчик).
Исправить "перекос" можно разрезав одну ветку на две и "привив" образовавшиеся половинки к новому гнезду, содержащему условие, определяющее: в какой из веток следует искать сравниваемую переменную. Например, левая ветка может содержать гнезда с четными значениями, а правая – с нечетными. Но это плохой критерий: четных и нечетных значений редко бывает поровну и вновь образуется перекос (тем не менее никакого произвола нет и для балансировки можно использовать любой подходящий алгоритм).
Гораздо надежнее поступить так: берем наименьшее из всех значений и бросаем его в кучу А, затем берем наибольшее из всех значений и бросаем его в кучу B. Так повторяем до тех пор, пока не рассортируем все, имеющиеся значения.
Поскольку, оператор множественного выбора требует уникальности каждого значения, т.е. каждое число может встречаться в наборе (диапазоне) значений лишь однажды, легко показать, что: а) в обеих кучах будет содержаться равное количество чисел (в худшем случае – в одной куче окажется на одно число больше); б) все числа кучи A меньше наименьшего из чисел кучи B. Следовательно, достаточно выполнить только одно сравнение, чтобы определить: в какой из двух куч следует искать сравниваемое значения.
Высота нового дерева будет равна , где N – количество гнезд старого дерева. Действительно, мы же делим ветвь дерева надвое и добавляем новое гнездо – отсюда и берется и +1, а (N+1) необходимо для округления результата деления в большую сторону. Т.е. если высота не оптимизированного дерева достигала 100 гнезд, то теперь она уменьшилась до 51. Что? Говорите, 51 все равно много? А что нам мешает разбить каждую из двух ветвей еще на две? Это уменьшит высоту дерева до 27 гнезд! Аналогично, последующее уплотнение даст 16 à
12 à
11 à
9 à
8… и все! Более плотная упаковка дерева невозможна (подумайте почему – на худой конец постройте само дерево). Но, согласитесь, восемь гнезд – это не сто! Полное прохождение оптимизированного дерева потребует менее девяти сравнений!
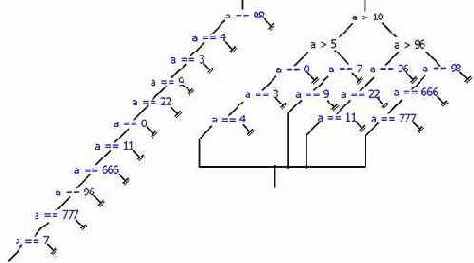
Рисунок 1 0х001 Логическое дерево до утрамбовки (слева) и после (справа)
Из всех трех рассматриваемых компиляторов "трамбовать" switch-и не умеет один лишь WATCOM, а Visual C++ и Borland C++ сполна справляются с этой задачей.