несбалансированное (слева) и сбалансированное (справа) switch/case-дерево
Высота вновь образованного дерева будет равна , где N – количество гнезд старого дерева. Действительно, мы же делим ветвь дерева надвое и добавляем новое гнездо – отсюда и берется и +1, а (N+1) необходимо для округления результата деления в большую сторону. Т. е. если высота не оптимизированного дерева достигала 100 гнезд, то теперь она уменьшилась до 51. Что? Говорите, 51 все равно много? Но кто нам мешает разбить каждую из двух ветвей еще на две? Это уменьшит высоту дерева до 27 гнезд! Аналогично, последующее уплотнение даст 16 à 12 à 11 à 9 à 8… и все! Более плотная упаковка дерева уже невозможна. Но, согласитесь, восемь гнезд – это не сто! Оптимизированный вариант оператора switch в худшем случае потребует лишь пяти сравнений, но и это еще не предел!
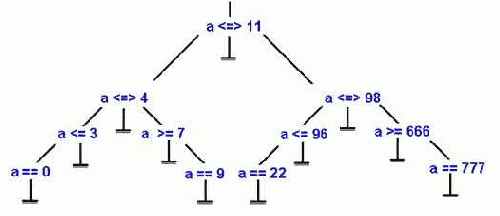
Учитывая, что x86 процессоры все три операции сравнения <, =, > совмещают в одной машинной команде, двоичное логическое дерево можно преобразовать в троичное, тогда новых гнезд для его балансировки добавлять не нужно. Простейший алгоритм, называемый методом отрезков, работает так: сортируем все числа по возрастанию и делим получившийся отрезок напополам. Число находящееся посередине (в нашем случае это 11), объявляем вершиной дерева, а числа расположенные слева от него — его левыми ветвями и подветвями (в нашем случае это 0, 3, 4 и 7). Остальные числа (22, 96, 98, 666, 777) идут направо. Повторяем эту операцию рекурсивно до тех пор, пока длина подветвей не сократится до единицы. В конечном счете, вырастет следующее дерево (см. рис. 2):