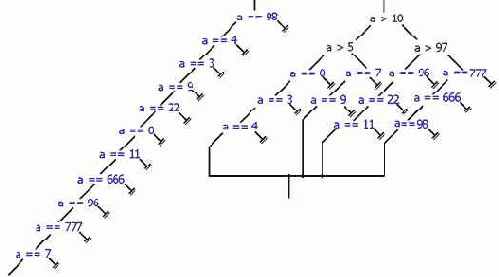
не оптимизированный вариант оператора множественно выбора
Тогда соответствующее ему не оптимизированное логическое дерево будет достигать в высоту одиннадцати гнезд (см. рис. 1 слева). Причем, на левой ветке корневого гнезда окажется аж десять других гнезд, а на правой – вообще ни одного. Чтобы исправить "перекос", разрежем одну ветку на две и прицепим образовавшиеся половинки к новому гнезду, содержащему условие, определяющее: в какой из веток следует искать сравниваемую переменную. Например, левая ветка может содержать гнезда с четными значениями, а правая – с нечетными. Но это плохой критерий: четных и нечетных значений редко бывает поровну и вновь образуется перекос. Гораздо надежнее поступить так: берем наименьшее из всех значений и бросаем его в кучу А, затем берем наибольшее из всех значений и бросаем его в кучу B. Так повторяем до тех пор, пока не рассортируем все, имеющиеся значения. (см. рис. 1 справа)
Поскольку, оператор switch требует уникальности каждого значения, т. е. каждое число может встречаться лишь однажды, легко показать, что: а) в обеих кучах будет содержаться равное количество чисел (в худшем случае – в одной куче окажется на число больше);
б) все числа кучи A меньше наименьшего из чисел кучи B. Следовательно, достаточно выполнить только одно сравнение, чтобы определить: в какой из двух куч следует искать сравниваемое значения.