Оптимизатор System R
Проект System R существенно улучшил состояние оптимизации запросов в реляционных системах. Идеи [55], внедренные во многие коммерческие оптимизаторы, продолжают оставаться удивительно современными. Я представлю здесь некоторые из этих важных идей в контексте запросов Select-Project-Join (SPJ). Класс SPJ-запросов тесно связан с конъюнктивными запросами, которые обычно изучаются в теории баз данных, и включает эти запросы.
Пространство поиска оптимизатора System R в контексте SPJ-запросов состоит из деревьев операций, которые соответствуют линейной последовательности операций соединения; например, последовательность Join (Join (Join (A,B),C),D) проиллюстрирована на рис. 2(a). Такие последовательности логически эквивалентны, поскольку соединения обладают свойствами ассоциативности и коммутативности. Для реализации операции соединения могут быть использованы методы вложенных циклов или сортировки и слияния. В каждом узле сканирования может использоваться индексное сканирование (на основе кластеризованного или некластеризованного индекса) или последовательное сканирование. Наконец, предикаты вычисляются как можно раньше.
Стоимостная модель присваивает оценочную стоимость любому частичному или полному плану в пространстве поиска. Она также определяет оценочный размер потока данных для вывода каждой операции плана. Эти оценки базируются на следующем:
Кроме того, проверяется также, не будут ли иметь какой-то порядок данные в выходном потоке.
В оценочной модели механизмы (a)-(c) используются для вычисления для операций плана и связывания с этими операциями следующей информации (вычисления и связывание происходят в направлении от листьев к корню дерева):
- Размер выходного потока данных узла-операции.
- Любая упорядоченность кортежей, создаваемая или сохраняемая в выходном потоке данных узла-операции.
- Оценочная стоимость выполнения операции (и общая стоимость произведенного к этому моменту частичного плана).
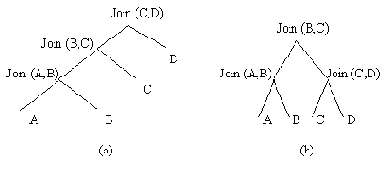
Рис. 2. Линейное (a) и кустовое (b) соединения
Алгоритм перебора в оптимизаторе System R демонстрирует два важных метода: использование динамического программирования и использование интересных упорядочений.
Суть подхода динамического программирования основывается на предположении, что оценочная модель удовлетворяет принципам оптимальности. Более точно, предполагается, что для получения оптимального плана SPJ-запроса Q, состоящего из k соединений, достаточно рассматривать только оптимальные планы для подвыражений Q, которые состоят из (k-1) соединений, и расширять эти планы добавочным соединением. Другими словами, для определения оптимального плана выполнения Q не требуется рассматривать не самые оптимальные планы для подвыражений Q (называемых также подзапросами) с (k-1) соединениями. Соответственно, основанный на динамическом программировании алгоритм перебора представляет SPJ-запрос Q как множество соединяемых отношений { R1, ..., Rn }. Алгоритм перебора работает снизу вверх. В конце j-го шага алгоритм производит оптимальные планы для всех подзапросов размера j. Для получения оптимального плана для подзапроса, включающего (j+1) соединение, мы рассматриваем все возможные способы конструирования плана путем расширения планов, построенных на j-ом шаге. Например, оптимальный план для { R1, R2, R3, R4 } получается выбора плана с наименьшей стоимостью из оптимальных планов для:
Остальные планы для {R1, R2, R3, R4} можно отбросить. Подход динамического программирования работает существенно быстрее, чем "наивный" перебор, поскольку требуется перебрать O(n2n-1) планов вместо O(n!).
Вторым важным аспектом оптимизатора System R является рассмотрение интересных упорядочений. Рассмотрим теперь запрос, представляющий соединение между {R1, R2, R3} с предикатами R1.a = R2.b = R3.c. Предположим, что стоимости планов для подзапроса {R1, R2} оценены в x и y для методов вложенных циклов и сортировки и слияния соответственно, и x < y. В таком случае при рассмотрении плана для {R1, R2, R3} мы не принимаем во внимание план, согласно которому R1 и R2 соединяются методом сортировки и слияния. Однако заметим, что если для соединения R1 и R2 используется метод сортировки и слияния, то результат соединения упорядочен по a. Этот порядок сортировки может существенно уменьшить стоимость соединения с R3. Следовательно, отбрасывание плана, включающего соединение сортировкой и слиянием R1 и R2, может привести к неоптимальности глобального плана. Проблема возникает по той причине, что в выходном потоке результата соединения R1 и R2 имеется упорядоченность кортежей, которая полезна для последующего соединения. Однако соединение методом вложенных циклов не обеспечивает такого упорядочения. Поэтому для заданного запроса System R определяет порядок кортежей, который потенциально важен для планов выполнения запроса (отсюда название "интересные упорядочения"). К тому же, в оптимизаторе System R два плана являются сравнимыми только в том случае, когда они представляют одно и то же выражение и, кроме того, обеспечивают одно и то же интересное упорядочение. Идея интересных упорядочений позже была обобщена до идеи физических свойств [22] и интенсивно используется в современных оптимизаторах. На интуитивном уровне физическое свойство - это любая характеристика плана, не являющаяся общей для всех планов одного и того же выражения, но могущая влиять на последующие операции.Наконец, заметим, что подход System R принятия во внимание физических свойств демонстрирует простой механизм управления любым отклонением от принципа оптимальности, не обязательно связанным с физическими свойствами.
Несмотря на элегантность подхода System R, этот подход невозможно расширить для включения других логических преобразований (в добавление к изменению порядка соединений), расширяющих пространство поиска. Это привело к разработке более расширяемых архитектур оптимизации. Однако использование оптимизации на основе оценочной стоимости, динамического программирования и интересных упорядочений сильно повлияло на последующие разработки в области оптимизации.
- -