Разбиение на классы ячеек
Идея этого алгоритма состоит в том, чтобы вместо хранения всех ячеек куба хранить только классы ячеек с одинаковым значением агрегирующей функции. Если же указать выпуклое разбиение (т.е. если две ячейки
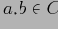
и
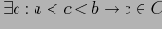
), достаточно будет хранить только верхние и нижние грани классов, т.к. все ячейки класса можно будет вывести из этих границ.
Однако разбиение только по значению агрегирующей функции разрушает семантику куба (и тем более не выпукло). Покажем это.
Например, рассмотрим еще раз таблицу Продажи из введения (). Получившиеся разбиение изображено на рис. .
 |
Разбиение только по значению агрегирующей функции
У нас получается следующая схема (рисунок ).
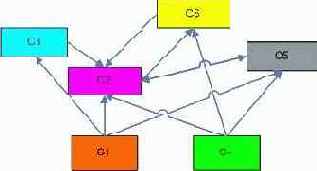 |
Выбор агрегирующей функции в данном случае не важен, т.к. у нас есть возможность двигаться в обе стороны по отношениям roll-up/drill-down. Например, можно пойти вверх от ячейки (ALL, ALL, ALL) в С2 в ячейку (ALL, книги, ALL) в C5, а потом в (R2, книги, ALL) в С2. Тем самым, нарушается семантика отношений roll-up/drill-down.
Таким образом, мы показали, что разбиение только по значению агрегирующей функции не порождает связанной решетки классов эквивалентности. Необходимы какие-то ограничения.
В первых работах по данному алгоритму в качестве разбиения предлагалось так называемое связанное разбиение, однако оно верно только для монотонных функций (Sum (слагаемые одного знака), Count и пр). Впоследствии было предложено разбиение по покрытию. Поэтому здесь в примерах используется AVG — немонотонная функция.
Будем рассматривать кортежи куба как решетку (CL(r), Cube Lattice над отношением r) с введенным порядком, определенным иерархиями измерений (т.е.
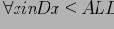
). Введем определение покрытия для решетки (см [1],[2])
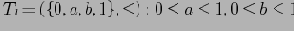
.
Определение 5.2 Будем говорить, что в частично упорядоченном множестве
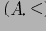
элемент а покрывает элемент b, или b покрывается элементом a (обозначение:
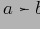
или
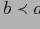
), если:
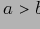

, такого, что
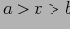
Следующая лемма показывает, что отношение покрываемости будет определять частичный порядок на множестве.
Лемма 1 Если
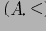
— конечное частично упорядоченное множество, то
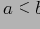
тогда и только тогда, когда
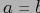
, или когда существует конечная последовательность элементов
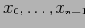
такая, что
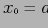
,
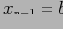
и
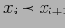
для
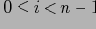
. Отношение покрываемости в решетке

будет выглядеть следующим образом:
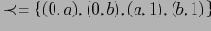
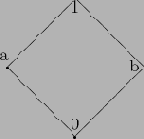
На диаграмме частично упорядоченного множества
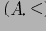
элементы изображаются в виде маленьких кружочков

; кружки, соответствующие элементам x и у, соединяются прямой линией тогда и только тогда, когда один из них покрывает другой; если x покрывает y, то кружок, соответствующий элементу x, помещается выше кружка, соответствующего элементу y. Отметим, что в диаграмме пересечение двух линий не обозначает элемент. Диаграмма для решетки

изображена на рисунке .
 |
Кортеж
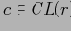
покрывает базовый (фактический) кортеж
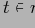
, если
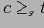
. Определение 5.4 Отношение эквивалентности по покрытию
Определим отношение эквивалентности
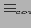
как транзитивное и рефлексивное замыкание

, где:
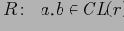
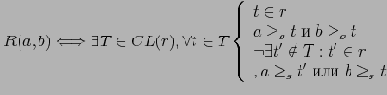
Введенные определения и теоремы позволяют утверждать, что разбиение по покрытию формирует полную решетку куба, только ячейками этой решетки будут являться классы ячеек обычной решетки. Причем у каждого класса будет существовать верхняя и нижняя грань, решетка будет связанной и выпуклой. Значения всех дистрибутивных и алгебраических функций для всех ячеек подобного класса эквивалентности будет совпадать.
Рассмотрим тот же пример, только на этот раз разбиение будет вестись по покрытию (рис. ).
Рис. 5.4:
Разбиение по покрытию
Соответствующая решетка по классам показана на рис. .
Рис. 5.5:
Классы разбиения по покрытию
Таким образом, для получившегося куба нам нужно хранить только две ячейки на класс, верхнюю и нижнюю грань. Остальные ячейки выводятся из верхней и нижней грани, т.к. классы разбиения по покрытиям''полны'' в смысле введенного частичного порядка.
Для Quotient Cube предложено две структуры хранения данных: QC - Tables [12] и QC-Trees [11].
QC-Table — простая таблица, в которой для каждого класса хранится верхняя и нижняя грань. Предложены алгоритмы создания QC-Table и вставки/удаления классов. Такие таблицы неэффективны по времени обработки запросов, т.к. каждый запрос требует просмотра почти всей таблицы.