Condensed Cube

В основу этого алгоритма легло наблюдение о возрастающей ''разреженности'' кубов (см. также ). Т.е. с возрастанием числа измерений и иерархий в них, процентное соотношение объема начальных данных к объему всех данных, которые необходимо в общем случае хранить, все возрастает. Рассмотрим граничный пример. Пусть у нас есть отношение R, содержащее только один кортеж

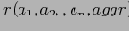
. Тогда результирующий куб будет содержать

кортежей:

где

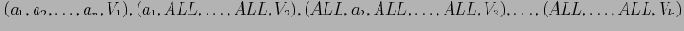
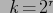
Так как в отношении содержится только один кортеж, все

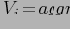
. Следовательно, можно физически хранить только один кортеж

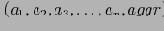
вместе с какой-то служебной информацией, отмечающей, что этот кортеж является ''представителем'' множества кортежей. И для любых запросов по подкубам, нам достаточно возвращать агрегирующее значение изначального кортежа, без каких-либо дальнейших вычислений.

Этот алгоритм обладает рядом следующих отличительных черт.

''Сжатый куб'' (Condensed Cube) не сжимается. Следовательно, несмотря на то, что он обладает меньшим размером по сравнению с полным кубом, это не влияет на выполнение запросов (он не требует разархивирования перед обработкой запросов).

''Сжатый куб'' полностью вычислен. В отличие от многих подходов, предлагающих лишь частичные вычисления подкубов, в данном подходе результатом является полностью вычисленный куб.

''Сжатый куб'' содержит абсолютно точные агрегирующие значения в отличие от различных аппроксимирующих методов.

''Сжатый куб'' удовлетворяет базовым требованиям к OLAP-данным и поддерживает все OLAP приложения в отличие от методов, предлагающих уменьшение размера кубов за счет ограничения возможных запросов.

Ключевым понятием этого алгоритма является ''базовый единичный кортеж'' (Base Single Tuple) — кортеж, который является единственным, формирующим агрегирующие отношения.

Кортежи куба группируются (разбиваются) и агрегируются из базового отношения. В общем случае в любом из разбиений существует большое количество кортежей базового отношения, особенно в подкубах с малым числом измерений. Однако существуют разбиения, содержащие только один кортеж.
Подобные кортежи в дальнейшем называются ''базовыми единичными кортежами''.

Определение 5.1 Пусть

— набор измерений.

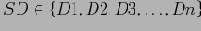
. Если

— единственный кортеж в разбиении , образованом по

, то

- базовый единичный кортеж по

, и

— синглетное множество для

. Далее, делается вывод, что если кортеж является базовым единичным кортежем по

, то он является базовым единичным кортежем для любого ''надмножества''

. Кортеж может быть базовым единичным кортежем для нескольких наборов измерений, т.е. для случаев разных группировок ячеек куба возможно существование нескольких срезов, содержащих только одним этот кортеж базовой таблицы. Таким образом, с каждым кортежем связывается множество наборов типа

. При этом на всех разбиениях из

агрегирующие значения на любых возможных функциях равны. В дальнейшем, при создании куба эти наблюдения учитываются, и в порожденном кубе все возможные дубликаты базового единичного кортежа удаляются, что приводит к сокращению объема данных и, соответственно, времени выполнения запросов. Для этого вместе с каждой ячейкой хранится служебная информация, указывающая на

этой ячейки и, анализатор запросов учитывает данную информацию при обработке.

Вперед: Quotient Cube

Выше: Семантические алгоритмы

Назад: Семантические алгоритмы

Содержание раздела

Главная сайта