Алгоритм Star-Cubing
Алгоритм Star-Cubing, представленный в работе [13], предназначен для вычисления кубов типа айсберг. В алгоритме сочетаются агрегирование "снизу-вверх" и "сверху-вниз", многопозиционное агрегирование (как в ) и применение леммы Apriori (как в ). Данные хранятся в специальной структуре star-tree, эффективно сжимающей данные, что позволяет сократить время расчета и объем потребляемых ресурсов.
На уровня подкубов используется агрегирование снизу-вверх, однако существует уровень обнаружения разделяемых измерений, в котором работа идет сверху-вниз. Подобное сочетание позволяет алгоритму агрегировать по нескольким измерением одновременно, разделяя затраты на агрегирование и используя для отсечения подкубов, не удовлетворяющих условию MinSup .
Последовательность вычислений в алгоритме Star-Cubing проиллюстрирована на рисунке , описывающем вычисление четырехмерного куба ABCD. Если бы использовалась только вычисление снизу-вверх, то подкубы, помеченные словом "отсечено", были бы вычислены. Star-Cubing может отсечь указанные подкубы, принимая в расчет разделяемые измерения. Здесь ACD/A означает, что подкуб ACD имеет разделяемое измерение А, ABD/AB — подкуб AB имеет разделяемое измерение AB, ABC/ABC — подкуб ABC имеет разделяемое измерение ABC и т.д. Таким образом, все подкубы ветви, начинающейся с ACD, включают измерение A, ветви, начинающейся с ABD,- измерение AB, ветви, начинающейся с ABC,- измерение ABC. Подобные измерения называются разделяемыми для соответствующих ветвей.
Схема работы алгоритма Star-Cubing, обработка подкубов снизу-вверх и использование разделяемых измерений
Поскольку разделяемые измерения можно обнаружить в самом начале вычисления дерева подкубов, можно избежать перевычисления подобных измерений в дальнейшем. К примеру, подкуб AB, вычисляемый из ABD, отсечен, т.к. уже вычислен в ABD/AD. Аналогично отсекается куб A, вычислимый из AD, т.к. уже вычислен ACD/A.
Напомним, что необходимым условием использования является дистрибутивность используемой агрегирующей функции.
К примеру, если в разделяемом измерении А значение

не удовлетворяет условию MinSup, то отсекается вся ветвь от
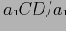
(включая
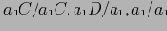
), поскольку эти ячейки заведомо не удовлетворяют условию MinSup.
Прежде чем приступить к примеру работы алгоритма, введем несколько понятий.
В алгоритме для представления индивидуальных подкубов используются деревья. На рисунке
изображена часть дерева куба для подкуба ABCD. Каждый уровень дерева представляет собой измерение, и каждый узел представляет собой значение атрибута. Каждый узел имеет 4 поля: значение аттрибута, агрегированное значение, указатель/указатели на потомков и указатель/указатели на элементы того же уровня. Кортежи подкуба вставляются в дерево один за другим. Путь от корня к листу представляет собой кортеж. К примеру, агрегированное значение (по мере count) узла

в дереве равно 5, что означает 5 ячеек значения
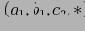
. Подобное представление позволяет сократить пространство, требуемое для хранения общих префиксов (см. также ), и хранить агрегированные значения в внутренних узлах, что позволяет на этапе вычисления отсекать ветви, основанные на разделяемых измерения. К примеру, дерево подкуба AB может быть использовано для отсечения возможных ячеек в ABD.
Рис. 4.3:
Фрагмент дерева одного из базовых подкубов
Если агрегированое значение, допустим p, не удовлетворяет условию, то бесполезно различать подобные узлы в процессе вычисления куба. Поэтому узел p можно заменить *, еще больше сжимая таким образом дерево. Будем называть узел р узлом-звездой (star-node), если агрегированное значение по измерению в точке p не удовлетворяет условию MinSup. Дерево подкуба, сжатое с помощью узлов-звезд, будем называть деревом звезд (star-tree).
Рассмотрим пример построения дерева-звезд.
 |
Предположим MinSup = 2, тогда только значения
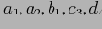
удовлетворяют условию. Все прочие значения превращаются в узлы-звезды. После отбрасывания узлов-звезд получается таблица . Отметим, что эта таблица содержит меньше кортежей и различных значений, нежели исходная таблица фактов. Поэтому для построения подкуба мы будем использовать эту таблицу. Получившееся дерево звезд изображено на рисунке , а таблица узлов-звезд — на таблице . Для выделения узлов-звезд используются таблицы звезд (от англ star-table) для каждого дерева. Пример таблицы подобной таблицы для описанного выше случая приведен на рисунке . Более эффективно использовать битовые массивы или хэш таблицы для таблиц звезд.
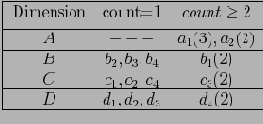 |
 |
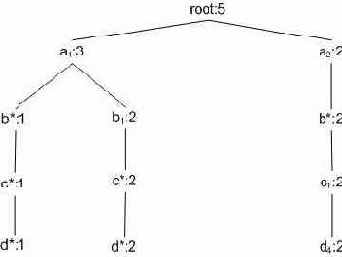 |
 |
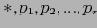
на каждом уровне.
Рассмотрим на этом же примере примере, как в работе Star-Cubing алгоритма используются деревья-звезды.
При агрегировании используется дерево-звезд типа того, которое изображено на рисунке . Агрегирование начинается снизу-вверх, при этом используется алгоритм поиска в глубину. Первый этап вычислений (т.е. обработка первой ветви дерева) изображен на рис . В левой части рисунка показано основное дерево звезд. Для каждого значения атрибута изображено агрегированное значение этого узла. Подстрочный номер указывает порядок обхода узлов. Остаются деревья BCD, ACD/A, ABD/AB, ABC/ABC, потомки основного дерева звезд, отвечающие за уровень выше базового на рисунке . Подстрочные номера вновь указывают на порядок обхода.
Например, на первом шаге алгоритма создается корневой узел дерева-потомка BCD, на втором — корневой узел дерева ACD/A, на третьем — корневой узел ABD/AB и узел b*.
Рис. 4.5:
Первый этап агрегирования: обработка левой ветви базового дерева
Рис. 4.6:
Второй этап агрегирования: обработка второй ветви базового дерева
В правой части рисунка показаны деревья в памяти на 5-ом шаге алгоритма. Поскольку к этому моменту поиск в глубину достигает листа дерева, происходит возврат. До возврата алгоритм отмечает, что все возможные узлы базового измерения ABC уже были просмотрены. Это значит, что дерево ABC/ABC уже просмотрено, и результат равен count, а дерево можно удалить. Аналогично, двигаясь назад от d* к c* и принимая во внимание, что у c* нет потомков, алгоритм устанавливает, что count в ABD/AB является финальным результатом, и дерево удаляется.
При возврате в вершине b*, поскольку существует одноуровневый узел

, дерево ACD/A будет сохранено в памяти, и поиск в глубину пойдет от вершины

, так же, как до этого от b*. Результирующие деревья изображены на рисунке . Деревья потомки ACD/A и ABD/A создаются заново, со значениями из поддерева

. К примеру, агрегированное значение с* в ACD/D возрастает от 1 до 3. Деревья остаются неизменными, к ним лишь добавляются новые ветви либо увеличиваются агрегированные значения. Например, дополнительная ветвь добавляется в дерево BCD.
По достижению листа d* алгоритм вновь возвращается, в этот раз до

, где будет замечен одноуровневый узел

. В этом случае будут удалены все деревья, кроме BCD на рисунке . После этого аналогичный обход будет совершен для

. Дерево BCD продолжает расти, а остальные деревья начинаются с корня в

.
Для того, чтобы у узла были потомки, необходимо выполнение двух условий:
Это необходимо, поскольку, если все узлы будут тривиальными, ни один из них не будет удовлетворять условию MinSup, и вычислять их будет нецелесообразно.
Подобное отсечение проиллюстрированно на рисунках.
Производительность алгоритма Star- Cubing сильно зависит от порядка измерений, впрочем как и производительность прочих алгоритмов создания кубов типа айсберг. Наилучшая производительность достигается, если измерения обрабатываются в порядке убывания мощности, что повышает шансы отсечений ветвей на ранних этапах вычисления.
Star-Cubing также можно использовать и для полной материализации куба. При вычислении полного куба на плотном массиве данных производительность Star-Cubing сравнима с производительностью MultiWay и намного превосходит производительность BUC. В случае разреженных исходных данных StarCubing намного быстрее MultiWay и в большинстве случаев быстрее BUC. При вычислении кубов типа айсберг Star-Cubing быстрее BUC, если данные распеределены несимметрично, и разрыв в производительности увеличивается по мере уменьшения MinSup.
Вперед: Семантические алгоритмы
Выше: Вычисление Iceberg кубов
Назад: Алгоритм Bottom-Up Computation